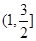题目内容
已知函数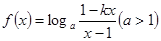 是奇函数,
是奇函数,
(1)求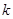 的值;
的值;
(2)在(1)的条件下判断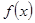 在
在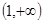 上的单调性,并运用单调性的定义予以证明.
上的单调性,并运用单调性的定义予以证明.
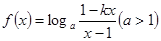 是奇函数,
是奇函数,(1)求
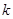 的值;
的值;(2)在(1)的条件下判断
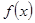 在
在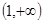 上的单调性,并运用单调性的定义予以证明.
上的单调性,并运用单调性的定义予以证明.(1) 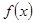 是奇函数,则
是奇函数,则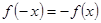 .
.
由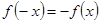
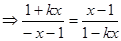
所以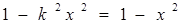
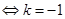 或
或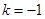 .………………………………5分
.………………………………5分
当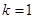 时,
时,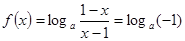 ,这与题设矛盾,
,这与题设矛盾,
当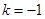 时,
时,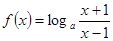 为奇函数,满足题设条件.…………………7分
为奇函数,满足题设条件.…………………7分
(2)在(1)的条件下,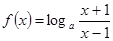 在
在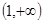 上是减函数,证明如下:
上是减函数,证明如下:
设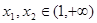 ,且
,且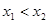 ,则
,则
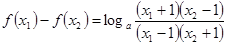
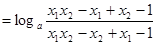 , ………………………………10分
, ………………………………10分
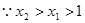
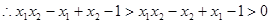 ,
,
即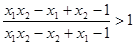 , ………………………………12分
, ………………………………12分
又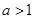 ,
,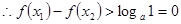
即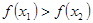 ,
,
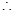
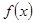 在
在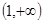 上是减函数.
上是减函数.
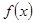 是奇函数,则
是奇函数,则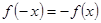 .
.由
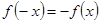
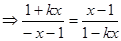
所以
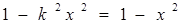
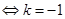 或
或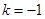 .………………………………5分
.………………………………5分当
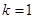 时,
时,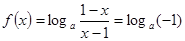 ,这与题设矛盾,
,这与题设矛盾, 当
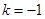 时,
时,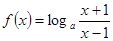 为奇函数,满足题设条件.…………………7分
为奇函数,满足题设条件.…………………7分(2)在(1)的条件下,
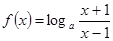 在
在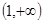 上是减函数,证明如下:
上是减函数,证明如下:设
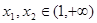 ,且
,且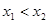 ,则
,则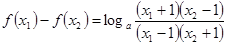
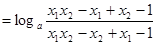 , ………………………………10分
, ………………………………10分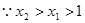
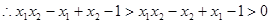 ,
,即
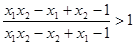 , ………………………………12分
, ………………………………12分又
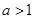 ,
,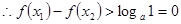
即
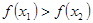 ,
,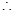
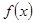 在
在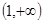 上是减函数.
上是减函数.略

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
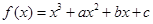 在
在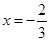 与
与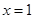 时都取得极值.若对
时都取得极值.若对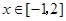 ,不等式
,不等式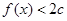 恒成立,则
恒成立,则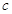 的取值范围是( )
的取值范围是( )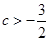
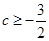
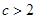
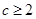
 在R上单调递增,设
在R上单调递增,设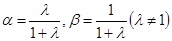 ,若有
,若有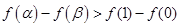 ,则
,则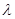 的取值范围是( )
的取值范围是( )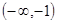
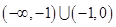
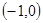
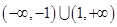
 的定义域为R,对任意
的定义域为R,对任意 ,均有
,均有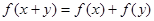 ,且对任意
,且对任意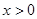 都有
都有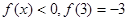 .
.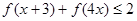 ;
;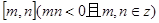 上的值域.
上的值域.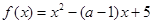 在区间
在区间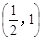 上是减函数,那么实数
上是减函数,那么实数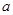 的取值范围是( ).
的取值范围是( ).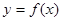 是定义在R上以
是定义在R上以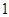 为周期的函数,若
为周期的函数,若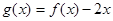 在区间
在区间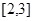 上的值域为
上的值域为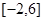 ,则函数
,则函数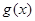 在
在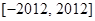 上的值域为
上的值域为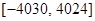
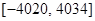
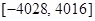
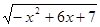 的单调增区间为( )
的单调增区间为( )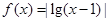 的单调递减区间是 。
的单调递减区间是 。 满足对任意的
满足对任意的 成立,那么a的取值范围是( )
成立,那么a的取值范围是( )