题目内容
已知M(1+cos2x,1), (x∈R,a∈R,a是常数),且
(x∈R,a∈R,a是常数),且 (其中O为坐标原点).
(其中O为坐标原点).(1)求y关于x的函数关系式y=f(x);
(2)求函数y=f(x)的单调区间;
(3)若
 时,f(x)的最大值为4,求a的值.
时,f(x)的最大值为4,求a的值.
【答案】分析:(1)利用向量数量积的定义可得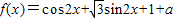
(2)利用和差角公式可得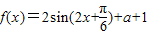 ,分别令
,分别令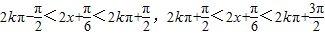
分别解得函数y=f(x)的单调增区间和减区间
(3)由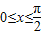 求得
求得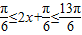 ,结合三角函数的性质求最大值,进而求出a的值
,结合三角函数的性质求最大值,进而求出a的值
解答:解:(1)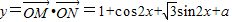 ,
,
所以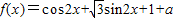 .
.
(2)由(1)可得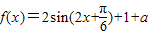 ,
,
由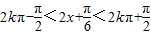 ,解得
,解得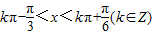 ;
;
由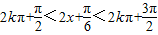 ,解得
,解得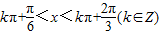 ,
,
所以f(x)的单调递增区间为 ,
,
单调递减区间为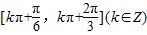 .
.
(3)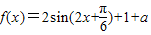 ,
,
因为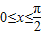 ,
,
所以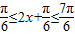 ,
,
当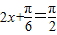 ,即
,即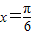 时,f(x)取最大值3+a,
时,f(x)取最大值3+a,
所以3+a=4,即a=1.
点评:本题以向量的数量积为载体考查三角函数y=Asin(wx+∅)的性质,解决的步骤是结合正弦函数的相关性质,让wx+∅作为整体满足正弦函数的中x所满足的条件,分别解出相关的量.
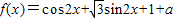
(2)利用和差角公式可得
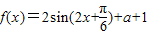 ,分别令
,分别令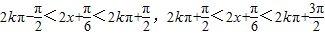
分别解得函数y=f(x)的单调增区间和减区间
(3)由
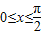 求得
求得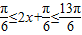 ,结合三角函数的性质求最大值,进而求出a的值
,结合三角函数的性质求最大值,进而求出a的值解答:解:(1)
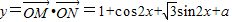 ,
,所以
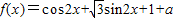 .
.(2)由(1)可得
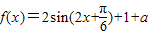 ,
,由
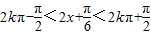 ,解得
,解得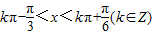 ;
;由
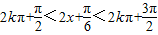 ,解得
,解得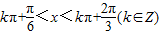 ,
,所以f(x)的单调递增区间为
 ,
,单调递减区间为
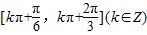 .
.(3)
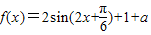 ,
,因为
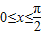 ,
,所以
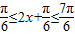 ,
,当
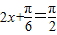 ,即
,即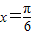 时,f(x)取最大值3+a,
时,f(x)取最大值3+a,所以3+a=4,即a=1.
点评:本题以向量的数量积为载体考查三角函数y=Asin(wx+∅)的性质,解决的步骤是结合正弦函数的相关性质,让wx+∅作为整体满足正弦函数的中x所满足的条件,分别解出相关的量.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
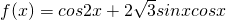 .
.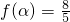 ,求cos2α的值.
,求cos2α的值.