题目内容
设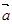 、
、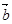 是不共线的两个非零向量.
是不共线的两个非零向量.
(1)若 ,求证:
,求证: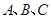 三点共线;
三点共线;
(2)若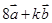 与
与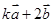 共线,求实数
共线,求实数 的值.
的值.
(1)证明详见解析;(2)当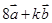 与
与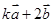 共线时,
共线时,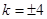 .
.
解析试题分析:(1)利用向量证明三点共线,先建立平面向量的基底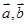 ,求出
,求出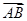 、
、 ,找到
,找到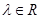 使得
使得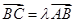 ,从而说明
,从而说明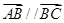 ,再说明两个向量有一个公共点
,再说明两个向量有一个公共点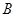 即可;(2)根据
即可;(2)根据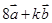 与
与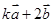 共线,得到
共线,得到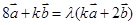 ,然后根据向量相等的条件,建立
,然后根据向量相等的条件,建立 、
、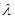 的方程组,求解即可得到
的方程组,求解即可得到 的值.
的值.
试题解析:(1)证明:∵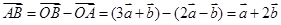
而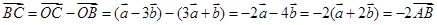
∴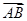 与
与 共线,又有公共端点
共线,又有公共端点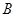 ,∴
,∴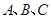 三点共线
三点共线
(2)∵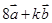 与
与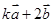 共线,∴存在实数
共线,∴存在实数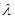 ,使得
,使得
∵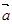 与
与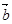 不共线
不共线
∴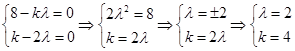 或
或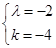
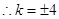 .
.
考点:1.向量共线定理;2.平面向量的基本定理;3.两向量相等的条件.

练习册系列答案
相关题目
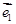 和
和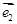 不共线.
不共线.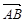 =
=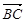 =
=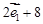
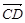 =
=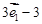
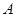 、
、 、
、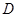 三点共线;
三点共线;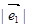 =2,
=2,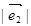 =3,
=3,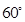 ,是否存在实数
,是否存在实数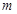 ,使得
,使得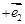 与
与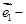
 ,
, 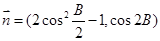 ,且
,且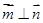 ,
,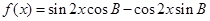 的单调减区间;
的单调减区间;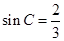 ,求
,求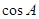 .
.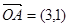 ,
,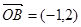 ,
,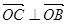 ,
,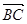 ∥
∥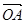 ,试求满足
,试求满足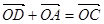 的
的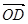 的坐标(O为坐标原点)。
的坐标(O为坐标原点)。 ,点
,点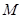 为
为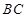 的中点,点
的中点,点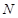 满足
满足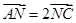 ,点
,点 满足
满足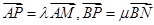 .
.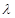 与
与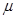 的值;
的值;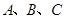 三点坐标分别为
三点坐标分别为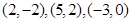 ,求
,求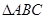 ,角
,角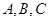 所对的边分别为
所对的边分别为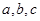 ,向量
,向量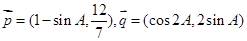 ,且
,且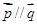 。
。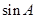 的值;(2)若
的值;(2)若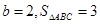 ,求
,求 的值。
的值。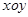 中,
中,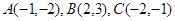 .
.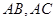 为邻边的平行四边形的两条对角线的长;
为邻边的平行四边形的两条对角线的长;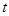 满足
满足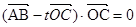 ,求
,求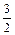 ,sinα),b=(cosα,
,sinα),b=(cosα,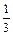 ),且a// b,则锐角α为 ___________________
),且a// b,则锐角α为 ___________________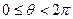 ,已知两个向量
,已知两个向量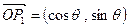 ,
,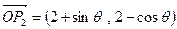 ,则向量
,则向量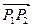 长度的最大值是
长度的最大值是