题目内容
(理)实数x,y满足x2-y2=4,若
+m>0恒成立,则实数m的取值范围为______.
| y+2 |
| x |
∵
+m>0恒成立
∴m>-
恒成立,则只要m>-
的最大值即可
令k=
,则k的几何意义是在双曲线上任取一定与定点A(0,-2)的连线的斜率
联立方程
可得(1-k2)x2+4kx-8=0
∴△=16k2+32(1-k2)≥0
∴-
≤k≤
∴-
≤-
≤
即-
的最大值为
故答案为:m≥
| y+2 |
| x |
∴m>-
| y+2 |
| x |
| y+2 |
| x |
令k=
| y+2 |
| x |
联立方程
|
∴△=16k2+32(1-k2)≥0
∴-
| 2 |
| 2 |
∴-
| 2 |
| y+2 |
| x |
| 2 |
| y+2 |
| x |
| 2 |
故答案为:m≥
| 2 |

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
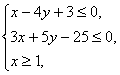 目标函数z=kx+y的最大值为12,最小值为3,那么实数k的值为
目标函数z=kx+y的最大值为12,最小值为3,那么实数k的值为 那么2y-x的最大值为
那么2y-x的最大值为