题目内容
(理)实数x,y满足x2-y2=4,若
+m>0恒成立,则实数m的取值范围为
| y+2 |
| x |
m≥
| 2 |
m≥
.| 2 |
分析:由题意可得m>-
恒成立,则只要m>-
的最大值即可,令k=
,则k的几何意义是在双曲线上任取一定与定点A(0,-2)的连线的斜率,联立方程
可得(1-k2)x2+4kx-8=0,由△=16k2+32(1-k2)≥0可求K的最大值进而可求m的范围
| y+2 |
| x |
| y+2 |
| x |
| y+2 |
| x |
|
解答:解:∵
+m>0恒成立
∴m>-
恒成立,则只要m>-
的最大值即可
令k=
,则k的几何意义是在双曲线上任取一定与定点A(0,-2)的连线的斜率
联立方程
可得(1-k2)x2+4kx-8=0
∴△=16k2+32(1-k2)≥0
∴-
≤k≤
∴-
≤-
≤
即-
的最大值为
故答案为:m≥
| y+2 |
| x |
∴m>-
| y+2 |
| x |
| y+2 |
| x |
令k=
| y+2 |
| x |
联立方程
|
∴△=16k2+32(1-k2)≥0
∴-
| 2 |
| 2 |
∴-
| 2 |
| y+2 |
| x |
| 2 |
| y+2 |
| x |
| 2 |
故答案为:m≥
| 2 |
点评:本题主要考查了直线与曲线相交关系的应用,在解题时,关键是分析表达式的几何意义,把恒成立问题转化为求解式子的最大值的问题,还要注意本题的转化思想的应用.

练习册系列答案
相关题目
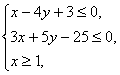 目标函数z=kx+y的最大值为12,最小值为3,那么实数k的值为
目标函数z=kx+y的最大值为12,最小值为3,那么实数k的值为 那么2y-x的最大值为
那么2y-x的最大值为