题目内容
已知![]() ,其中向量
,其中向量![]() ,(
,(![]() R).
R).
(1) 求![]() 的最小正周期和最小值;
的最小正周期和最小值;
(2) 在△ ABC中,角A、B、C的对边分别为![]() 、
、![]() 、
、![]() ,若
,若![]() ,a=2
,a=2![]() ,
,![]() 求边长
求边长![]() 的值.
的值.
解:(1) f(x)=a·b-1=(sin2x,2cosx)·(![]() ,cosx)-1
,cosx)-1
=![]() sin2 x +2cos2 x -1=
sin2 x +2cos2 x -1=![]() sin2x+cos2x=2sin(2x+
sin2x+cos2x=2sin(2x+![]() )
)
∴f(x)的最小正周期为π,最小值为-2.
(2) f(![]() )=2sin(
)=2sin(![]() +
+![]() )=
)=![]()
∴sin(![]() +
+![]() )=
)=![]()
∴![]() +
+![]() =
=![]() ∴ A=
∴ A=![]() 或
或![]() (舍去)
(舍去)
由余弦定理得a2=b2+c2-2bccosA
52=64+c2-8c即c2-8c+12=0
从而c=2或c=6

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 ,其中向量
,其中向量 , (
, ( R).
R). 的最小正周期和最小值;
的最小正周期和最小值; 、
、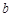 、
、 ,若
,若 ,a=2
,a=2 ,
, ,求边长
,求边长 的值.
的值. ,其中向量
,其中向量 ,(
,( R).
R). 的最小正周期和最小值;
的最小正周期和最小值; 、
、 、
、 ,若
,若 ,a=2
,a=2 ,
, ,求边长
,求边长 的值.
的值.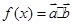 ,其中向量
,其中向量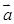 =
= ,
,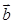 =
=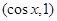 (x∈R)
(x∈R)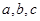 ,
,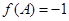 ,
,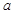 =
=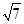 ,
,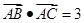 ,求边长b和c的值(b>c)。
,求边长b和c的值(b>c)。