题目内容
已知函数f（x）=x3+sinx，x（-1，1），如果f（1-m）+f（1-m2）＜0，则m的取值范围是________．
（1，
）
分析：确定函数为增函数、奇函数，再化不等式为具体不等式，即可求m的取值范围．
解答：求导函数可得：f′（x）=3x2+cosx
∵x∈（-1，1），∴f′（x）＞0
∴函数f（x）为增函数
∵f（-x）=（-x）3+sin（-x）=-x3-sinx=-f（x）
∴函数f（x）为奇函数
∵f（1-m）+f（1-m2）＜0，
∴f（1-m）＜f（m2-1），
∴
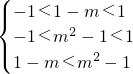
∴1＜m＜
故答案为：（1，）．
点评：本题考查函数的单调性与奇偶性，解题的关键是确定函数的单调性与奇偶性，属于中档题．
）分析：确定函数为增函数、奇函数，再化不等式为具体不等式，即可求m的取值范围．
解答：求导函数可得：f′（x）=3x2+cosx
∵x∈（-1，1），∴f′（x）＞0
∴函数f（x）为增函数
∵f（-x）=（-x）3+sin（-x）=-x3-sinx=-f（x）
∴函数f（x）为奇函数
∵f（1-m）+f（1-m2）＜0，
∴f（1-m）＜f（m2-1），
∴
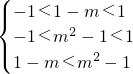
∴1＜m＜
故答案为：（1，
）．点评：本题考查函数的单调性与奇偶性，解题的关键是确定函数的单调性与奇偶性，属于中档题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
单元加期末复习先锋大考卷系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|