Question

（03年全国卷）（14分）

已知常数，在矩形ABCD中，，，O为AB的中点，点E、F、G分别在BC、CD、DA上移动，且，P为GE与OF的交点（如图），问是否存在两个定点，使P到这两点的距离的和为定值？若存在，求出这两点的坐标及此定值；若不存在，请说明理由

Answer 1

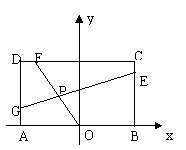
解析：根据题设条件，首先求出点P坐标满足的方程，据此再判断是否存在两定点，使得点P到定点距离的和为定值.

按题意有A（－2，0），B（2，0），C（2，4a），D（－2，4a）

设，

由此有E（2，4ak），F（2－4k，4a），G（－2，4a－4ak）.

直线OF的方程为：，        ①

直线GE的方程为：.　　②

从①，②消去参数k，得点P（x，y）坐标满足方程，

整理得.

当时，点P的轨迹为圆弧，所以不存在符合题意的两点.

当时，点P轨迹为椭圆的一部分，点P到该椭圆焦点的距离的和为定长.

当时，点P到椭圆两个焦点的距离之和为定值.

当时，点P到椭圆两个焦点的距离之和为定值.