题目内容
S是空间四边形ABCD的对角线BD上任意一点,E、F分别在AD、CD上,且AE∶AD=CF∶CD,BE与AS相交于R,BF与SC相交于Q.求证:EF∥RQ.

证明:在ΔADC中,因AE∶AD=CF∶CD,故EF∥AC,
而AC 平面ACS,故EF∥平面ACS.
平面ACS,故EF∥平面ACS.
而RQ=平面ACS∩平面RQEF,
故EF∥RQ(线面平行性质定理).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(3)直线与平面垂直的性质
| 类别 | 语言表述 | 图示 | 字母表示 | 作用 |
| 性质 | (1)若一条直线与一个平面垂直,则这条直线垂直于平面内的__ 直线 |
|
| 证两条直线垂直 |
| (2)如果两条直线__________一个平面,那么这两条直线平行 |
|
| 证两条直线平行 |
 、
、 、
、 ,求这个长方体的对角线长与体积
,求这个长方体的对角线长与体积 已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( ) B.
B.
 D.
D.
 B.
B. C.
C. D.
D.

 序号是( )
序号是( )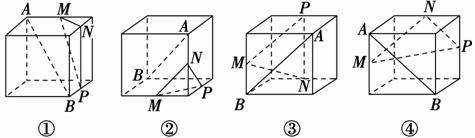
 C.②③ D.②④
C.②③ D.②④



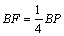 ,C是弧AB的中点.
,C是弧AB的中点.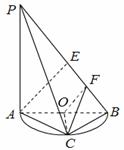 (1)证明:BC^平面PAC;
(1)证明:BC^平面PAC; 的定义域为R,命题q:不等式
的定义域为R,命题q:不等式 的解集为
的解集为 ,若“p∧q”为假命题且“p∨q”为真命题,求实数a的取值范围.
,若“p∧q”为假命题且“p∨q”为真命题,求实数a的取值范围.