题目内容
已知数列{an}和数列{bn},数列{an}的前n项和记为sn,a1=1,an+1=2sn+1(n≥1),点(35n-4•an,bn)在对数函数y=log3x的图象上.
(1)求数列{bn}的通项公式;
(2)设cn=
,Tn是数列{cn}的前n项和,求使Tn<
对所有n∈N*都成立的最小正整数m.
(1)求数列{bn}的通项公式;
(2)设cn=
| 3 |
| bn•bn+1 |
| m |
| 20 |
解(1)由an+1=2sn+1可得an=2sn-1+1(n≥2),
两式相减得an+1-an=2an,即an+1=3an(n≥2),又a2=2s1+1=3,所以a2=3a1,
故{an}是首项为1,公比为3的等比数列,
所以an=3n-1,
所以bn=log3(35n-4•an)=log3(35n-4•3n-1)=6n-5(n∈N*)….(7分)
(2)∵cn=
=
=
(
-
),…..(9分)
所以Tn=
[(1-
)+(
-
)+…(
-
)]=
(1-
)…..(11分)
因此,使得
(1-
)<
(n∈N*)成立的m必须且仅须满足
≤
,
即m≥10,满足要求的最小整数m为10…..(14分)
两式相减得an+1-an=2an,即an+1=3an(n≥2),又a2=2s1+1=3,所以a2=3a1,
故{an}是首项为1,公比为3的等比数列,
所以an=3n-1,
所以bn=log3(35n-4•an)=log3(35n-4•3n-1)=6n-5(n∈N*)….(7分)
(2)∵cn=
| 3 |
| bn•bn+1 |
| 3 |
| (6n-5)(6n+1) |
| 1 |
| 2 |
| 1 |
| 6n-5 |
| 1 |
| 6n+1 |
所以Tn=
| 1 |
| 2 |
| 1 |
| 7 |
| 1 |
| 7 |
| 1 |
| 13 |
| 1 |
| 6n-5 |
| 1 |
| 6n+1 |
| 1 |
| 2 |
| 1 |
| 6n+1 |
因此,使得
| 1 |
| 2 |
| 1 |
| 6n+1 |
| m |
| 20 |
| 1 |
| 2 |
| m |
| 20 |
即m≥10,满足要求的最小整数m为10…..(14分)

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
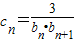 ,Tn是数列{cn}的前n项和,求使
,Tn是数列{cn}的前n项和,求使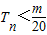 对所有n∈N*都成立的最小正整数m.
对所有n∈N*都成立的最小正整数m.