题目内容
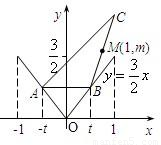
如图是函数y=A sin（wx+φ）（A＞0，w＞0），|φ|＜π的图象，由图中条件，写出该函数解析式
分析：由图象直接求出A和T，可求w，根据特殊点（π，0）结合|φ|＜π求出φ，即可求函数f（x）的解析式；
解答：解：由图象知A=5，T=3π，
∵T=
=3π，∴w=
．
又∵图象经过点（π，0），
∴5sin（
+φ）=0．
∵|φ|＜π，∴φ=
，
∴f（x）=5sin（
x+
）．
故答案为：y=5sin（
x+
）．
∵T=
| 2π |
| w |
| 2 |
| 3 |
又∵图象经过点（π，0），
∴5sin（
| 2π |
| 3 |
∵|φ|＜π，∴φ=
| π |
| 3 |
∴f（x）=5sin（
| 2 |
| 3 |
| π |
| 3 |
故答案为：y=5sin（
| 2 |
| 3 |
| π |
| 3 |
点评：本题考查三角函数y=Asin（ωx+φ）的图象及其解析式，考查学生的视图用图能力，是基础题．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
浙江之星学业水平测试系列答案
相关题目
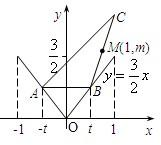如图，函数y=
|x|在x∈［－1,1］的图像上有两点A、B，AB∥Ox轴，点M(1，m)(m∈R且m>
|x|在x∈[－1,1]的图象上有两点A、B，AB∥
如图，函数y=
|x|在x∈[-1，1]的图象上有两点A，B，AB∥Ox轴，点M（1，m）（m是已知实数，且m＞
|x|在x∈[-1，1]的图象上有两点A，B，AB∥Ox轴，点M（1，m）（m是已知实数，且m＞
）是△ABC的边BC的中点．