题目内容
已知f(x)=a1x+a2x2+a3x3+…+anxn,n为正偶数,且a1,a2,a3,…,an组成等差数列,又f(1)=n2,f(-1)=n.试比较f( )与3的大小.
)与3的大小.
解:∵f(1)=a1+a2++an=n2.
依题设,有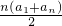 =n2,故a1+an=2n,
=n2,故a1+an=2n,
即2a1+(n-1)d=2n.
又f(-1)=-a1+a2-a3+a4-a5+-an-1+an=n,
∴ •d=n,有d=2.进而有2a1+(n-1)2=2n,解出a1=1.
•d=n,有d=2.进而有2a1+(n-1)2=2n,解出a1=1.
于是f(1)=1+3+5+7++(2n-1).
f(x)=x+3x2+5x3+7x4++(2n-1)xn.
∴f( )=
)= +3(
+3( )2+5(
)2+5( )3+7(
)3+7( )4++(2n-1)(
)4++(2n-1)( )n.①
)n.①
①两边同乘以 ,得
,得 f(
f( )=(
)=( )2+3(
)2+3( )3+5(
)3+5( )4++(2n-3)(
)4++(2n-3)( )n+(2n-1)(
)n+(2n-1)( )n+1.②
)n+1.②
①-②,得 f(
f( )=
)= +2(
+2( )2+2(
)2+2( )3++2(
)3++2( )n-(2n-1)(
)n-(2n-1)( )n+1,
)n+1,
即 f(
f( )=
)= +
+ +(
+( )2++(
)2++( )n-1-(2n-1)(
)n-1-(2n-1)( )n+1.
)n+1.
∴f( )=1+1+
)=1+1+ +
+ ++
++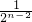 -(2n-1)
-(2n-1) =1+
=1+ -(2n-1)
-(2n-1) =1+2-
=1+2-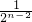 -(2n-1)
-(2n-1) <3.
<3.
∴f( )<3.
)<3.
分析:由题设条件可知2a1+(n-1)d=2n.再由f(-1)=-a1+a2-a3+a4-a5+-an-1+an=n可解出a1=1.所以f( )=
)= +3(
+3( )2+5(
)2+5( )3+7(
)3+7( )4+…+(2n-1)(
)4+…+(2n-1)( )n,再用错位相减法求解即可.
)n,再用错位相减法求解即可.
点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.
依题设,有
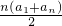 =n2,故a1+an=2n,
=n2,故a1+an=2n,即2a1+(n-1)d=2n.
又f(-1)=-a1+a2-a3+a4-a5+-an-1+an=n,
∴
 •d=n,有d=2.进而有2a1+(n-1)2=2n,解出a1=1.
•d=n,有d=2.进而有2a1+(n-1)2=2n,解出a1=1.于是f(1)=1+3+5+7++(2n-1).
f(x)=x+3x2+5x3+7x4++(2n-1)xn.
∴f(
 )=
)= +3(
+3( )2+5(
)2+5( )3+7(
)3+7( )4++(2n-1)(
)4++(2n-1)( )n.①
)n.①①两边同乘以
 ,得
,得 f(
f( )=(
)=( )2+3(
)2+3( )3+5(
)3+5( )4++(2n-3)(
)4++(2n-3)( )n+(2n-1)(
)n+(2n-1)( )n+1.②
)n+1.②①-②,得
 f(
f( )=
)= +2(
+2( )2+2(
)2+2( )3++2(
)3++2( )n-(2n-1)(
)n-(2n-1)( )n+1,
)n+1,即
 f(
f( )=
)= +
+ +(
+( )2++(
)2++( )n-1-(2n-1)(
)n-1-(2n-1)( )n+1.
)n+1.∴f(
 )=1+1+
)=1+1+ +
+ ++
++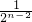 -(2n-1)
-(2n-1) =1+
=1+ -(2n-1)
-(2n-1) =1+2-
=1+2-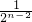 -(2n-1)
-(2n-1) <3.
<3.∴f(
 )<3.
)<3.分析:由题设条件可知2a1+(n-1)d=2n.再由f(-1)=-a1+a2-a3+a4-a5+-an-1+an=n可解出a1=1.所以f(
 )=
)= +3(
+3( )2+5(
)2+5( )3+7(
)3+7( )4+…+(2n-1)(
)4+…+(2n-1)( )n,再用错位相减法求解即可.
)n,再用错位相减法求解即可.点评:本题考查数列的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 )与3的大小.
)与3的大小.