题目内容
已知函数f（x）=xlnx
（Ⅰ）求f（x）的单调区间；
（Ⅱ）设函数f（x）的最小值为M，求与曲线y=f（x）相切且斜率为e•M（其中e为常数）的切线方程．
解：（I）函数的定义域为：（0，+∞）
对函数求导可得f′（x）=lnx+1
令f′（x）＞0可得
f′（x）＜0可得
则函数的单调增区间为（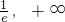
），单调减区间为（0，
）
（II）由（I）可知函数x=取得最小值，故M=f（）=
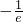，e•M=-1
设满足条件的切点为（x0，y0），则根据导数的几何意义有lnx0+1=-1即
切点坐标为（
切线方程为
分析：（I）先求函数的定义域，然后对函数求导可得f′（x）=lnx+1分别令f′（x）＞0f′（x）＜0可求函数的单调增区间，单调减区间
（II）由（I）可知函数x=取得最小值，从而可求故M=f（），e•M=-1
设满足条件的切点为（x0，y0），则根据导数的几何意义可求切点坐标为（，进一步可得切线方程
点评：（1）想要求函数的单调区间，可先求函数的定义域，然后结合导数的符号进行求解，此类问题容易忽略对定义域的判断
（2）利用导数的几何意义设出切点坐标是解决该问题的关键
对函数求导可得f′（x）=lnx+1
令f′（x）＞0可得
f′（x）＜0可得
则函数的单调增区间为（
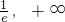），单调减区间为（0，）（II）由（I）可知函数x=
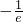取得最小值，故M=f（）=，e•M=-1设满足条件的切点为（x0，y0），则根据导数的几何意义有lnx0+1=-1即
切点坐标为（
切线方程为
分析：（I）先求函数的定义域，然后对函数求导可得f′（x）=lnx+1分别令f′（x）＞0f′（x）＜0可求函数的单调增区间，单调减区间
（II）由（I）可知函数x=
取得最小值，从而可求故M=f（），e•M=-1设满足条件的切点为（x0，y0），则根据导数的几何意义可求切点坐标为（
，进一步可得切线方程点评：（1）想要求函数的单调区间，可先求函数的定义域，然后结合导数的符号进行求解，此类问题容易忽略对定义域的判断
（2）利用导数的几何意义设出切点坐标是解决该问题的关键
练习册系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|