题目内容
(文科)在等比数列{an}中,已知a1+a2=3,a3+a4=6.(1)求a9+a10;(2)求a10+a11+a12+a13.
【答案】分析:设出此等比数列的公比为q,根据等比数列的性质得: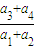 =q2列出关于q的方程,求出方程的解得到公比q的值,
=q2列出关于q的方程,求出方程的解得到公比q的值,
(1)根据等比数列的性质化简得a9+a10=(a1+a2)•q8,把a1+a2及q的值代入即可求出值;
(2)根据等比数列的性质化简得a10+a11+a12+a13=(a1+a2+a3+a4)q9,把a1+a2,a3+a4,及q的值代入即可求出值.
解答:解:∵{an}为等比数列,设公比为q,
∴q2=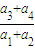 =
= =2,解得:q=±
=2,解得:q=± ,(4分)
,(4分)
(1)a9+a10=(a1+a2)•q8=3×24=16×3=48;(8分)
(2)a10+a11+a12+a13=(a1+a2+a3+a4)q9=(3+6)•(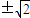 )9=±9•16
)9=±9•16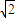 =±144
=±144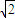 .(12分)
.(12分)
点评:此题考查了等比数列的通项公式,以及等比数列的性质,利用了整体代入的思想,灵活运用等比数列的性质是解本题的关键.
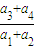 =q2列出关于q的方程,求出方程的解得到公比q的值,
=q2列出关于q的方程,求出方程的解得到公比q的值,(1)根据等比数列的性质化简得a9+a10=(a1+a2)•q8,把a1+a2及q的值代入即可求出值;
(2)根据等比数列的性质化简得a10+a11+a12+a13=(a1+a2+a3+a4)q9,把a1+a2,a3+a4,及q的值代入即可求出值.
解答:解:∵{an}为等比数列,设公比为q,
∴q2=
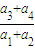 =
= =2,解得:q=±
=2,解得:q=± ,(4分)
,(4分)(1)a9+a10=(a1+a2)•q8=3×24=16×3=48;(8分)
(2)a10+a11+a12+a13=(a1+a2+a3+a4)q9=(3+6)•(
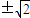 )9=±9•16
)9=±9•16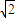 =±144
=±144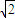 .(12分)
.(12分)点评:此题考查了等比数列的通项公式,以及等比数列的性质,利用了整体代入的思想,灵活运用等比数列的性质是解本题的关键.

练习册系列答案
相关题目