Question

16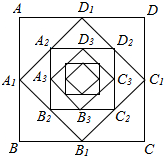．如图，正方形ABCD的边长为1，联结这个正方形各边的中点得到一个小正方形A₁B₁C₁D₁；又联结这个小正方形各边的中点得到一个更小的正方形A₂B₂C₂D₂；如此无限继续下去，设各正方形的边长依大小顺序构成数列{a_n}．
（1）写出a₂，a₃，a₄；
（2）猜想数列{a_n}的通项公式，请说明理由；并求出所有正方形的周长之和．

Answer 1

分析 （1）a₂=|A₁D₁|=$\sqrt{（\frac{1}{2}）^{2}+（\frac{1}{2}）^{2}}$=$\frac{\sqrt{2}}{2}$，同理可得a₃=$\frac{1}{2}$，a₄=$\frac{\sqrt{2}}{4}$．
（2）猜想a_n=${2}^{\frac{1-n}{2}}$．证明如下：由于当n≥2时，${a}_{n}=\frac{\sqrt{2}}{2}{a}_{n-1}$．利用等比数列的通项公式即可得出．再利用等比数列的前n项和公式即可得出：所有正方形的周长之和．

解答 解：（1）a₂=|A₁D₁|=$\sqrt{（\frac{1}{2}）^{2}+（\frac{1}{2}）^{2}}$=$\frac{\sqrt{2}}{2}$=${2}^{-\frac{1}{2}}$，a₃=$\sqrt{（\frac{\sqrt{2}}{4}）^{2}×2}$=$\frac{1}{2}$=2^-1，a₄=$\sqrt{（\frac{1}{4}）^{2}×2}$=$\frac{\sqrt{2}}{4}$=${2}^{-\frac{3}{2}}$．
（2）猜想a_n=${2}^{\frac{1-n}{2}}$．证明如下：
由于当n≥2时，${a}_{n}=\frac{\sqrt{2}}{2}{a}_{n-1}$．
∴数列{a_n}是等比数列，首项为1，公比为$\frac{\sqrt{2}}{2}$，∴a_n=$（\frac{\sqrt{2}}{2}）^{n-1}$=${2}^{\frac{1-n}{2}}$．
所有正方形的周长之和=$4×\frac{1-（\frac{\sqrt{2}}{2}）^{n}}{1-\frac{\sqrt{2}}{2}}$=（8+4$\sqrt{2}$）$[1-（\frac{\sqrt{2}}{2}）^{n}]$．

点评 本题考查了等比数列的通项公式及其前n项和公式，考查了猜想归纳推理能力与计算能力，属于中档题．