Question

【题目】如图， 中， ， 分别是 的中点，将 沿 折起成 ，使面 面 ， 分别是 和 的中点，平面 与 ， 分别交于点 .

（1）求证： ；
（2）求二面角 的正弦值.

Answer 1

【答案】
（1）证明：∵ 分别是 的中点，∴ ，而 平面 ， 平面 ，
∴ 平面
又平面 平面 ，故
（2）解：如图，建立空间直角坐标系，由题意得：

， ， ， ， ，
∴ ， ， ， ，
设平面 的一个法向量为 ，
则 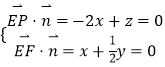，令 ，解得 ，
∴
设平面 的一个法向量为 ，
则 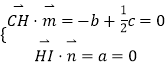，取 ，得 ，
设二面角 的平面角为 ，
则 ，∴ .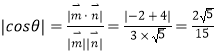
∴二面角 的正弦值为
【解析】(1)利用中位线证明 D E / / B C，从而得到线面平行，再利用线面平行的性质证出I H / / B C。
（2）利用空间向量，建立空间直角坐标，利用方程组求出两个半平面的法向量，再求出法向量夹角余弦值，进而求出正弦值。