题目内容

精英家教网已知倾斜角α≠0的直线l过椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点交椭圆于A、B两点，P为右准线上任意一点，则∠APB为（　　）
A、钝角B、直角
C、锐角D、都有可能
分析：根据题设条件推导出以AB为直径的圆与右准线相离．由此可知∠APB为锐角．
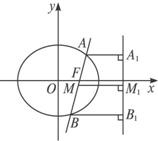
解答：解：如图，设M为AB的中点，过点M作MM1垂直于准线于点M1，分别过A、B作AA1、BB1垂直于准线于A1、B1两点．
则|MM1|=
|AA1|+|BB1|
2
=
|AF|
e
+
|BF|
e
2
=
|AB|
2e
＞
|AB|
2
.
∴以AB为直径的圆与右准线相离．
∴∠APB为锐角．
点评：本题考查圆锥曲线的性质和应用，解题时作出图形，数形结合，往往能收到事半功倍之效果．
练习册系列答案
相关题目
已知L为过点P(-
3
3
2
，-
3
2
)且倾斜角为30°的直线，圆C为圆心是坐标原点且半径等于1的圆，Q表示顶点在原点而焦点是(
2
8
，0)的抛物线，设A为L和C在第三象限的交点，B为C和Q在第四象限的交点．
（1）写出直线L、圆C和抛物线Q的方程，并作草图．
（2）写出线段PA、圆弧AB和抛物线上OB一段的函数表达式．
（3）设P′、B′依次为从P、B到x轴的垂足，求由圆弧AB和直线段BB′、B′P′、P′P、PA所包含的面积．

（本小题满分12分）已知椭圆过点A（a,0）,B(0,b)的直

 

线倾斜角为，原点到该直线的距离为.

 

（1）求椭圆的方程；

（2）斜率小于零的直线过点D（1，0）与椭圆交于M，N两点，若求直线MN的方程；

（3）是否存在实数k，使直线交椭圆于P、Q两点，以PQ为直径的圆过点D（1，0）？若存在，求出k的值；若不存在，请说明理由。

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网