题目内容
20．已知f（x）=$\left\{\begin{array}{l}{-x，x＞0}\\{{x}^{2}，x＜0}\end{array}\right.$，则f[f（x）]=（ ）| A． | $\left\{\begin{array}{l}{{x}^{2}，x＞0}\\{-{x}^{2}，x＜0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{-{x}^{2}，x＞0}\\{{x}^{2}，x＜0}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{-x，x＞0}\\{{x}^{2}，x＜0}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{-x，x＜0}\\{{x}^{2}，x＞0}\end{array}\right.$ |
分析 直接利用分段函数化简求解即可．
解答 解：f（x）=$\left\{\begin{array}{l}{-x，x＞0}\\{{x}^{2}，x＜0}\end{array}\right.$，
则x＞0时，f[f（x）]=f（-x）=（-x）2=x2．
x＜0时，f[f（x）]=f（x2）=-x2．
∴f[f（x）]=$\left\{\begin{array}{l}-{x}^{2}，x＞0\\{x}^{2}，x＜0\end{array}\right.$．
故选：B．
点评 本题考查分段函数的应用，函数解析式的求法，考查计算能力．
练习册系列答案
相关题目
在四面体ABCD中，AC=BD，E，F分别为AD，BC的中点，且EF=$\frac{\sqrt{2}}{2}$AC，∠BDC=90°，求证：BD⊥平面ACD．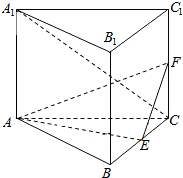
如图，直三棱柱ABC-A1B1C1的底面是边长为2的正三角形，E，F分别是BC，CC1的中点．