题目内容
10.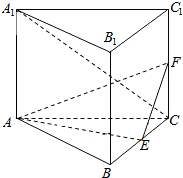 如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E,F分别是BC,CC1的中点.(1)证明:AE⊥平面BCC1B1;
(2)若AA1=$\sqrt{2}$,求三棱锥C-AEF的高.
分析 (1)首先证明AE⊥BB1,AE⊥BC,得到AE⊥平面BCC1B1;
(2)设三棱锥C-AEF的高为h,由VC-AEF=$\frac{1}{3}$S△ACE×CF=$\frac{1}{3}×$S△AEF×h,由勾股定理求得△AEF为Rt三角形,S△AEF=$\frac{1}{2}$AE×EF=$\frac{3\sqrt{2}}{4}$,即可解得h.
解答 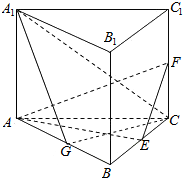 (1)证明:如图,因为三棱柱ABC-A1B1C1是直三棱柱,
(1)证明:如图,因为三棱柱ABC-A1B1C1是直三棱柱,
所以AE⊥BB1,
又E是正三角形ABC的边BC的中点,
所以AE⊥BC,
因此AE⊥平面BCC1B1;
(2)解:设三棱锥C-AEF的高为h,
∵AA1=$\sqrt{2}$,则AA1=BB1=CC1=2,CF=$\frac{\sqrt{2}}{2}$.
∴${S}_{△ACE}={\frac{1}{2}S}_{△ABC}=\frac{1}{2}×\frac{1}{2}×2×2×sin60°$=$\frac{\sqrt{3}}{2}$,
∴VC-AEF=$\frac{1}{3}$S△ACE×CF=$\frac{1}{3}×$S△AEF×h,
∵AE=$\sqrt{3}$,EF=$\frac{\sqrt{6}}{2}$,AF=$\frac{3\sqrt{2}}{2}$,
∴AE2+EF2=AF2=$\frac{9}{2}$,
∴△AEF为Rt三角形,
∴S△AEF=$\frac{1}{2}$AE×EF=$\frac{3\sqrt{2}}{4}$,
∴解得h=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查了直线与平面垂直的判定,考查了三棱柱体积的求法,考查了空间想象能力和推理论证能力,属于基本知识的考查.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
20.已知f(x)=$\left\{\begin{array}{l}{-x,x>0}\\{{x}^{2},x<0}\end{array}\right.$,则f[f(x)]=( )
| A. | $\left\{\begin{array}{l}{{x}^{2},x>0}\\{-{x}^{2},x<0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{-{x}^{2},x>0}\\{{x}^{2},x<0}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{-x,x>0}\\{{x}^{2},x<0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{-x,x<0}\\{{x}^{2},x>0}\end{array}\right.$ |
18.设i为虚数单位,则复数2-i的模为( )
| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 1 |
5.已知角α的终边经过点P(3,4),则角α的正切值是( )
| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |