题目内容
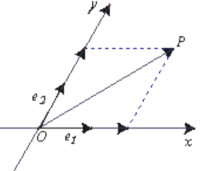
【题目】如图,设![]() 是平面内相交成
是平面内相交成![]() 角的两条数轴 ,
角的两条数轴 ,![]() 分别是
分别是![]() 轴,
轴,![]() 轴正方向同向的单位向量,若向量
轴正方向同向的单位向量,若向量![]() ,则把有序数对
,则把有序数对![]() 叫做向量
叫做向量![]() 在坐标系
在坐标系![]() 中的坐标,假设
中的坐标,假设![]() .
.
(1)计算![]() 的大小;
的大小;
(2)设向量![]() ,若
,若![]() 与
与![]() 共线,求实数
共线,求实数![]() 的值;
的值;
(3)是否存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,若存在求出
垂直,若存在求出![]() 的值,若不存在请说明理由.
的值,若不存在请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)先计算出![]() 的值,再根据公式
的值,再根据公式![]() ,求出
,求出![]() ;
;
(2)![]() ,由已知
,由已知![]() 与
与![]() 共线,根据向量共线的条件,可以得到等式,再根据平面向量基本定理,得到一个二元一次方程组,解这个方程组,可求出实数
共线,根据向量共线的条件,可以得到等式,再根据平面向量基本定理,得到一个二元一次方程组,解这个方程组,可求出实数![]() 的值;
的值;
(3)假设存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,则有:
垂直,则有:![]() ,根据平面向量数量积的运算公式,可以得到一个关于
,根据平面向量数量积的运算公式,可以得到一个关于![]() 的方程,如果能解出方程,就说明存在,如果方程没有实数根,就说明不存在.
的方程,如果能解出方程,就说明存在,如果方程没有实数根,就说明不存在.
(1) ![]() ,
,
所以![]()
![]()
![]()
![]() ;
;
(2)![]() 若
若![]() 与
与![]() 共线,则存在实数
共线,则存在实数![]() 使得
使得
![]() 即
即![]() ,由平面向量基本定理得:
,由平面向量基本定理得:
![]() ,解得
,解得![]()
所以实数![]() 的值
的值![]()
(3)假设存在实数![]() ,使得
,使得![]() 与向量
与向量![]() 垂直,则有:
垂直,则有:![]()
即![]()
![]()
![]()
![]() ,得
,得![]()
所以,存在实数![]() , 使得
, 使得![]() 与向量
与向量![]() 垂直.
垂直.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
