题目内容
时钟经过一小时,时针转过的弧度数为 ( )
A. rad rad | B. rad rad | C. rad rad | D. rad rad |
D
解析试题分析:时钟经过一小时,时针转过的角是周角的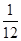 ,且为负角,所以时针转过的弧度数为
,且为负角,所以时针转过的弧度数为 ,故选D。
,故选D。
考点:本题主要考查角的概念,弧度制。
点评:简单题,注意顺时针旋转形成的角是负角,逆时针旋转形成的角是正角。

练习册系列答案
相关题目
角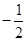 的终边过点P(4,-3),则
的终边过点P(4,-3),则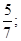 的值为( )
的值为( )
| A.4 | B.-3 | C.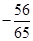 | D.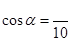 |
若2弧度的圆心角所对的弧长为4cm,则这个圆心角所夹的扇形的面积是( )
| A.4 cm2 | B.2 cm2 | C.4πcm2 | D.2πcm2 |
为了使函数y=sinωx(ω>0)在区间[0,1]上至少出现50次最大值,则ω的最小值是( ).
| A.98π | B.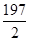 π π | C.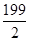 π π | D.100π |
函数 的部分图象如图,则
的部分图象如图,则 、
、 可以取的一组值是( )
可以取的一组值是( )
A.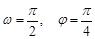 | B. |
C. | D. |
设 ,则
,则
A. | B. | C. | D. |
已知 为第二象限角,
为第二象限角, 为第二象限角,
为第二象限角, ,则
,则
A. | B. | C. | D. |
sin(- p)= ( )
p)= ( )
A. | B.? | C.? | D. |
已知函数 ,则方程
,则方程 所有根的和为( )
所有根的和为( )
| A.0 | B. | C. | D. |