题目内容
若2弧度的圆心角所对的弧长为4cm,则这个圆心角所夹的扇形的面积是（ ）
| A．4 cm2 | B．2 cm2 | C．4πcm2 | D．2πcm2 |
A
解析试题分析：结合弧长公式，求圆的半径，再利用扇形的面积公式，可得结论．解：弧度是2的圆心角所对的弧长为4，所以根据弧长公式，可得圆的半径为2，所以扇形的面积为：
×4×2=4cm2，故选A
考点：扇形的弧长公式与扇形的面积公式
点评：本题考查扇形的弧长公式与扇形的面积公式，属于基础题
练习册系列答案
手拉手全优练考卷系列答案
相关题目
已知
，且
，则
的值是
A． | B． | C． | D． |
如果角
的终边经过点
，那么
的值是（ ）
A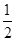． | B． | C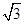． | D． |
若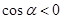
且
，则
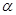是（ ）
| A．第一象限角 | B．第二象限角 | C．第三象限角 | D．第四象限角 |
函数
在一个周期内的图象如下，此函数的解析式为（ ）
A． | B． |
C． | D． |
如果1弧度的圆心角所对的弦长为2，那么这个圆心角所对的弧长为 （ ）
A． | B． | C． | D． |
的值（ ）
A．小于 | B．大于 | C．等于 | D．不存在 |
时钟经过一小时，时针转过的弧度数为 （ ）
A． rad | B． rad | C． rad | D． rad |
将函数
的图象向左平移
个单位, 再向上平移1个单位,所得图象的函数解析式是( )
A． +1 | B． | C． | D． |