题目内容
已知
<θ<πsin(
+θ)=-
,,则tan(π-θ)的值为( )
| π |
| 2 |
| π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
分析:首先根据诱导公式求出cosθ=-
,再根据角的范围求出θ的正弦值,进而根据诱导公式与同角三角函数关系得到答案.
| 3 |
| 5 |
解答:解:由题意可得:sin(
+θ)=-
,
所以cosθ=-
.
因为
<θ<π,
所以sinθ=
.
所以tan(π-θ)=-tanθ=
.
故选B.
| π |
| 2 |
| 3 |
| 5 |
所以cosθ=-
| 3 |
| 5 |
因为
| π |
| 2 |
所以sinθ=
| 4 |
| 5 |
所以tan(π-θ)=-tanθ=
| 4 |
| 3 |
故选B.
点评:本题主要考查同角三角函数间的基本关系,以及利用诱导公式求值.

练习册系列答案
相关题目
 如图,已知曲线
如图,已知曲线
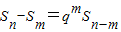 恒成立.
恒成立.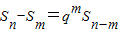 恒成立.
恒成立.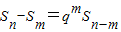 恒成立.
恒成立.