题目内容
设 ,
, ,
,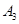 ,
, 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若 ,
, ,且
,且 ,则称
,则称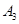 ,
, 调和分割
调和分割 ,
, ,已知点C(c,0),
,已知点C(c,0),
D(d,0) (c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
| A.C可能是线段AB的中点 | B.D可能是线段AB的中点 |
| C.C,D可能同时在线段AB上 | D.C,D不可能同时在线段AB的延长线上 |
D
解析试题分析:根据新定义, ,
, ,且
,且 ,则称
,则称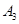 ,
, 调和分割
调和分割 ,
, 那么同时也知道
那么同时也知道 ,
, ,
,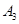 ,
, 四点共线,由于点C(c,0),
四点共线,由于点C(c,0),
D(d,0) (c,d∈R)调和分割点A(0,0),B(1,0),则可知(c,0)= (1,0),可知c=
(1,0),可知c= ,同理可知(d,0)=
,同理可知(d,0)= (1,0),d=
(1,0),d= ,由于
,由于 ,则可之
,则可之 ,那么可知,满足等式的点
,那么可知,满足等式的点 时,选项A成立。当
时,选项A成立。当 时,则选项B成立。当c=d=1,则可知选项C成立,排除法则选D.
时,则选项B成立。当c=d=1,则可知选项C成立,排除法则选D.
考点:本试题考查了向量的共线的运用。
点评:解决该试题的关键是对于已知中的向量的共线的理解和变形运用。通过给定的参数的关系式说明了点的位置情况,属于中档题。

练习册系列答案
相关题目
如图, 中,
中, ,
, ,
, 与
与 交于
交于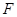 ,设
,设 ,
, ,
, ,则
,则 为( )
为( )
A. | B. | C. | D. |
四面体ABCD中,设M是CD的中点,则 化简的结果是( )
化简的结果是( )
A.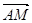 | B. | C. | D.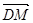 |
已知 =(3,4),
=(3,4), =(5,12),
=(5,12), 与
与 则夹角的余弦为( )
则夹角的余弦为( )
A. | B. | C. | D.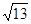 |
如图.点M是 的重心,则
的重心,则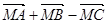 为( )
为( ) 
A. | B.4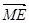 | C.4 | D.4 |
设 不共线,则下列四组向量中不能作为基底的是( )
不共线,则下列四组向量中不能作为基底的是( )
A. 与 与 | B. 与 与 |
C.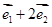 与 与 | D. 和 和 |
已知 是
是 的重心,
的重心, ,
, ,则
,则 的最小值是
的最小值是
A. | B. | C. | D.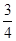 |
 = ( )
= ( )




 ,则k的值为 ( )
,则k的值为 ( )



