题目内容
【题目】双曲线
的左、右焦点分别是
，抛物线
的焦点与点
重合，点
是抛物线与双曲线的一个交点，如图所示.
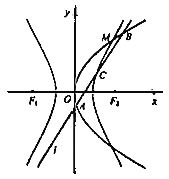
(1)求双曲线及抛物线的标准方程；
(2)设直线
与双曲线的过一、三象限的渐近线平行，且交抛物线于
两点，交双曲线于点
，若点是线段
的中点，求直线的方程.
【答案】（1）
，
（2）
【解析】分析：(1)先根据M坐标求p,得焦点坐标，再将M坐标代入双曲线方程，联立方程组解得a,b，(2)先求渐近线方程，设直线
方程，分别与抛物线方程、双曲线方程联立方程组，利用韦达定理以及中点坐标公式列方程，解得直线的方程.
详解：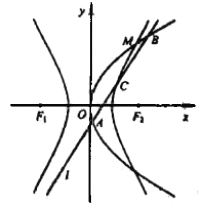
(1) 
代入
得
解得
因为焦点为
所以
，双曲线的焦点在
轴上
将
代入
所以
或
(舍去)
所以
所以她物线的标准方程为
曲线的标准方程为
(2)渐近线
设直线，
别消去
得
将
代入
得
，解得
或
，经验证，不合题意，故舍去.
所以
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
