题目内容
设M,m分别是f(x)在区间[a,b]上的最大值和最小值,则m(b-a)≤ f(x)dx≤M(b-a)由上述估值定理,估计定积分
f(x)dx≤M(b-a)由上述估值定理,估计定积分 的取值范围是 .
的取值范围是 .
【答案】分析:先求出函数f(x)=-x2在[-2,2]上的最大值和最小值,然后根据估值定理求出定积分的取值范围.
解答:解:f(x)=-x2在[-2,2]上的最小值m=-4,最大值为0
∴-4(2+2)≤ ≤0(2+2)
≤0(2+2)
即-16≤ ≤0
≤0
故答案为:[-16,0]
点评:本题主要考查了定积分的应用,以及新定义的概念,同时考查了阅读理解的能力,属于基础题.
解答:解:f(x)=-x2在[-2,2]上的最小值m=-4,最大值为0
∴-4(2+2)≤
 ≤0(2+2)
≤0(2+2)即-16≤
 ≤0
≤0故答案为:[-16,0]
点评:本题主要考查了定积分的应用,以及新定义的概念,同时考查了阅读理解的能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 f(x)dx≤M(b-a)由上述估值定理,估计定积分
f(x)dx≤M(b-a)由上述估值定理,估计定积分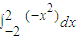 的取值范围是 .
的取值范围是 .