题目内容
 判断定义域为D的可导函数f(x)是否是“上凸函数”的流程图如图所示,则下列四个函数中是“上凸函数”的是
判断定义域为D的可导函数f(x)是否是“上凸函数”的流程图如图所示,则下列四个函数中是“上凸函数”的是
- A.y=2x
- B.y=x2
- C.y=2x
- D.y=lnx
D
分析:根据框图的要求先求原函数的导函数g(x),再求导函数的导函数h(x),在各自的定义域内判断好h(x)<0是否成立即可
解答:对于A:g(x)=(2x)'=2,h(x)=(2)'=0,不满足判断条件∴A不是“上凸函数”
对于B:g(x)=(x2)'=2x,h(x)=(2x)'=2>0,不满足判断条件∴B不是“上凸函数”
对于C:g(x)=(2x)'=2x•ln2,h(x)=(2x•ln2)'=(ln2)2•2x>0,不满足判断条件∴C不是“上凸函数”
对于D:g(x)=(lnx)'= ,h(x)=(
,h(x)=( )'=(x-1)'=-x-2=
)'=(x-1)'=-x-2= <0,满足判断条件∴D是“上凸函数”
<0,满足判断条件∴D是“上凸函数”
故选D
点评:本题考查导函数的求法,即求函数的值域.属简单题
分析:根据框图的要求先求原函数的导函数g(x),再求导函数的导函数h(x),在各自的定义域内判断好h(x)<0是否成立即可
解答:对于A:g(x)=(2x)'=2,h(x)=(2)'=0,不满足判断条件∴A不是“上凸函数”
对于B:g(x)=(x2)'=2x,h(x)=(2x)'=2>0,不满足判断条件∴B不是“上凸函数”
对于C:g(x)=(2x)'=2x•ln2,h(x)=(2x•ln2)'=(ln2)2•2x>0,不满足判断条件∴C不是“上凸函数”
对于D:g(x)=(lnx)'=
 ,h(x)=(
,h(x)=( )'=(x-1)'=-x-2=
)'=(x-1)'=-x-2= <0,满足判断条件∴D是“上凸函数”
<0,满足判断条件∴D是“上凸函数”故选D
点评:本题考查导函数的求法,即求函数的值域.属简单题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 判断定义域为D的可导函数f(x)是否是“上凸函数”的流程图如图所示,则下列四个函数中是“上凸函数”的是( )
判断定义域为D的可导函数f(x)是否是“上凸函数”的流程图如图所示,则下列四个函数中是“上凸函数”的是( )
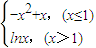 ,
, )是否是函数f(x)的“上线区间”(不必证明).
)是否是函数f(x)的“上线区间”(不必证明).