题目内容
(本小题16分)函数![]() 的定义域为{x| x ≠1},图象过原点,且
的定义域为{x| x ≠1},图象过原点,且![]() .
.
(1)试求函数![]() 的单调减区间;
的单调减区间;
(2)已知各项均为负数的数列![]() 前n项和为
前n项和为![]() ,满足
,满足![]() ,求证:
,求证:
![]() ;
;
(3)设![]() ,是否存在
,是否存在![]() ,使得
,使得![]()
![]() ?若存在,求出
?若存在,求出![]() ,证明结论;若不存在,说明理由.
,证明结论;若不存在,说明理由.
解:(1)由己知![]() .
.
![]() 且
且![]()
![]()
∴![]()
于是![]()
由![]() 得
得![]() 或
或![]()
故函数![]() 的单调减区间为
的单调减区间为![]() 和
和![]()
(2)由已知可得![]() ,
,
当![]() 时,
时,![]()
两式相减得![]()
∴![]() (各项均为负数)
(各项均为负数)
当![]() 时,
时,![]() , ∴
, ∴![]()
于是,待证不等式即为![]() .
.
为此,我们考虑证明不等式![]()
令![]() 则
则![]() ,
,![]()
再令![]() ,
,![]() 由
由![]() 知
知![]()
∴当![]() 时,
时,![]() 单调递增 ∴
单调递增 ∴![]() 于是
于是![]()
即![]() ①
①
令![]() ,
,![]() 由
由![]() 知
知![]()
∴当![]() 时,
时,![]() 单调递增 ∴
单调递增 ∴![]() 于是
于是![]()
即![]() ②
②
由①、②可知![]()
所以,![]() ,即
,即![]()
(3)![]() .
.
在![]() 中令
中令![]() 2010,并将各式相加得
2010,并将各式相加得
![]()
即![]() .
.

练习册系列答案
相关题目
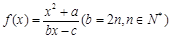 的定义域为{x| x ≠1},图象过原点,且
的定义域为{x| x ≠1},图象过原点,且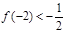 .
.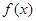 的单调减区间;
的单调减区间;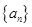 前n项和为
前n项和为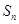 ,满足
,满足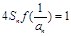 ,
,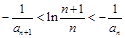 ;
;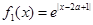 ,
,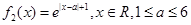 。
。 ,求使
,求使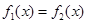 的
的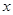 的值;
的值;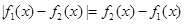 对于任意的实数
对于任意的实数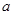 的取值范围;
的取值范围;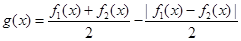 在
在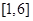 上的最小值.
上的最小值.