题目内容
(本小题16分)
已知函数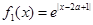 ,
,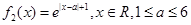 。
。
(1)若 ,求使
,求使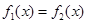 的
的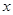 的值;
的值;
(2)若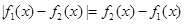 对于任意的实数
对于任意的实数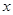 恒成立,求
恒成立,求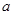 的取值范围;
的取值范围;
(3)求函数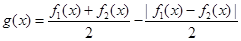 在
在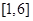 上的最小值.
上的最小值.
【答案】
(1) 
(2) 
(3) 
【解析】(1) ;
;
(2)即 恒成立,得
恒成立,得 ,即
,即 对
对 恒成立,因
恒成立,因 ,故只需
,故只需 ,解得
,解得 ,又
,又 ,故
,故 的取值范围为
的取值范围为 。
。
(3)
①当 时,由(2)知
时,由(2)知 ,当
,当 时,
时, 。
。
②当 时,
时, ,故
,故 。
。
 时,
时, ,
, ;
;
 时,
时, ,
, ;
;
 时,由
时,由 ,得
,得 ,其中
,其中 ,故当
,故当 时,
时, ;当
;当 时,
时, .
.
因此,当 时,
时,
令 ,得
,得 ,且
,且 ,如图,
,如图,

(ⅰ)当 ,即
,即 时,
时, ;
;
(ⅱ) 当 ,即
,即 时,
时, ;
;
(ⅲ) 当 ,即
,即 时,
时, 。
。
综上所述,

|

练习册系列答案
相关题目
 轴,焦点
轴,焦点 在直线
在直线 上,直线
上,直线 与抛物线相交于
与抛物线相交于 两点,
两点, 为抛物线上一动点(不同于
为抛物线上一动点(不同于 分别交该抛物线的准线
分别交该抛物线的准线 于点
于点 。
。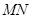 为直径的圆
为直径的圆 经过焦点
经过焦点
 ,
, ,
, , 点P的横坐标为14,且
, 点P的横坐标为14,且 ,点
,点 是边
是边 上一点,且
上一点,且 .
. 的值与点
的值与点 的坐标;
的坐标; 为线段
为线段 上的一个动点,试求
上的一个动点,试求 的取值范围.
的取值范围.