Question

△ABC的三边a，b，c满足b²=ac，且p=sinB+cosB，则p的取值范围是________．

Answer 1

分析：根据题意，由余弦定理可得cosB=，化简可得cosB=（+）-，结合基本不等式、余弦函数的性质可得≤cosB≤1，则B∈（0，60°]；由和差公式可得p=sinB+cosB=sin（B+45°），由正弦函数的性质，结合B+45°的范围，可得p的取值范围，
解答：根据题意，b²=ac，
由余弦定理可得cosB==（+）-，
又由+≥2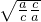=2，则cosB≥，
又由-1≤cosB≤1，
可得≤cosB≤1，则B∈[0，60°]，
p=sinB+cosB=sin（B+45°），
又由B∈（0，60°]，可得45°＜B+45°≤105°，
则1＜p≤，故p的取值范围是（1，]；
故答案为（1，]．
点评：本题考查余弦定理、基本不等式、正弦、余弦函数的性质以及和角公式的运用，关键是利用余弦定理和基本不等式求出角B的取值范围．