题目内容
19.已知1≤a≤3,2≤b≤5,则方程x2-bx+a2=0有实数解的概率是( )| A. | $\frac{3}{8}$ | B. | $\frac{2}{3}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{3}$ |
分析 本题考查的知识点是几何概型的意义,关键是要找出方程x2-2ax+b2=0有实数解对应的可行域面积的大小和实数a,b满足-1≤a≤1,-1≤b≤1对应的图形面积的大小
解答 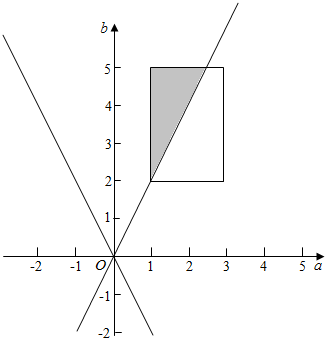 解:x2-bx+a2=0有实数解的充要条件是△=b2-4a2≥0.
解:x2-bx+a2=0有实数解的充要条件是△=b2-4a2≥0.
即$\left\{\begin{array}{l}{b+2a≥0}\\{b-2a≥0}\end{array}\right.$或$\left\{\begin{array}{l}{b+2a≤0}\\{b-2a≤0}\end{array}\right.$.
如下图所示,区域1≤a≤3,2≤b≤5的面积为6,
在1≤a≤3,2≤b≤5前提下,区域不等式组表示的区域面积为$\frac{1}{2}×3×(\frac{5}{2}-1)=\frac{9}{4}$,
由几何概型等式可得方程x2-bx+a2=0有实数解的概率是:$\frac{\frac{9}{4}}{6}=\frac{3}{8}$;
故选A.
点评 本题考查几何概型公式的运用;几何概型的概率估算公式中的“几何度量”,可以为线段长度、含面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.

练习册系列答案
相关题目
10.已知平面α与平面β相交于直线n,且不垂直,直线m?β,且m与n相交,点A∉α,l为过点A的一条动直线,那么下列情形可能出现的是( )
| A. | l∥m且l⊥α | B. | l⊥m且l⊥α | C. | l⊥m且l∥α | D. | l∥m且l∥α |
9.“a+b>0”是“任意的x∈[0,1],ax+b>0恒成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
 现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)
现有四种不同颜色的染料,给如图的四个不同区域染色,每个区域只染一种颜色,相邻区域染不同的颜色,不同颜色可重复使用,则共有108种不同分染色方法(用数字作答)