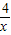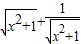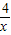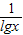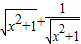题目内容
在下列函数中,当x取正数时,最小值为2的是( )
分析:A:直接利用基本不等式即可求解
B:当lgx<0时,函数不满足题意
C:令t=
,则t>1,y=
+
=t+
在(1,+∞)上单调递增,函数没有最小值
D:利用二次函数的性质可求函数的最小值
B:当lgx<0时,函数不满足题意
C:令t=
| x2+1 |
| x2+1 |
| 1 | ||
|
| 1 |
| t |
D:利用二次函数的性质可求函数的最小值
解答:解:∵x>0
A:y=x+
≥2
=4,即函数的最小值为4
B:当lgx<0时,函数不满足题意
C:令t=
,则t>1,y=
+
=t+
在(1,+∞)上单调递增,函数没有最小值
D:y=x2-2x+3=(x-1)2+2≥2,即函数的最小值为2
故选D
A:y=x+
| 4 |
| x |
x•
|
B:当lgx<0时,函数不满足题意
C:令t=
| x2+1 |
| x2+1 |
| 1 | ||
|
| 1 |
| t |
D:y=x2-2x+3=(x-1)2+2≥2,即函数的最小值为2
故选D
点评:本题主要考查了基本不等式、函数的单调性、二次函数的性质在求解函数的最值中的应用.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
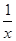 B.y=lgx+
B.y=lgx+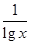
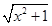 +
+ D.y=x2-2x+3
D.y=x2-2x+3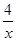 B.
B.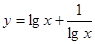
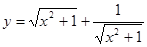 D.y=x2-2x+3
D.y=x2-2x+3