题目内容
【题目】若函数![]() 在(0, 2π)内有两个不同零点
在(0, 2π)内有两个不同零点![]() 、
、![]() 。
。
(1)求实数![]() 的取值范围;
的取值范围;
(2)求![]() 的值。
的值。
【答案】(1)a的取值范围是(-2, -![]() )∪(-
)∪(-![]() , 2).
, 2).
(2)![]() .
.
【解析】
(1)由于![]() ,故可将问题转化为方程sin(x+
,故可将问题转化为方程sin(x+![]() 在(0, 2π)内有相异二解,由条件得到
在(0, 2π)内有相异二解,由条件得到![]() ,结合函数的图象可得所求范围.(2)根据
,结合函数的图象可得所求范围.(2)根据![]() 、
、![]() 为函数
为函数![]() 的零点可得sinα+
的零点可得sinα+![]() cosα+
cosα+![]() =0且sinβ+
=0且sinβ+![]() cosβ+
cosβ+![]() =0,将两式相减并结合和差化积公式可得tan
=0,将两式相减并结合和差化积公式可得tan![]() ,从而可得所求.
,从而可得所求.
(1)由题意得sinx+![]() cosx=2(
cosx=2(![]() sinx+
sinx+![]() cosx)=2 sin(x+
cosx)=2 sin(x+![]() ),
),
∵函数![]() 在(0, 2π)内有两个不同零点,
在(0, 2π)内有两个不同零点,
∴关于x的方程sinx+![]() cosx+a=0在(0, 2π)内有相异二解,
cosx+a=0在(0, 2π)内有相异二解,
∴方程sin![]() 在(0, 2π)内有相异二解.
在(0, 2π)内有相异二解.
∵0<![]() 2π,
2π,
∴![]() .
.
结合图象可得若方程有两个相异解,则满足![]() 且
且![]() ,
,
解得![]() 且
且![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() .
.
(2) ∵ ![]() 是方程的相异解,
是方程的相异解,
∴ sinα+![]() cosα+
cosα+![]() =0 ①
=0 ①
sinβ+![]() cosβ+
cosβ+![]() =0 ②
=0 ②
①![]() ②得(sinα
②得(sinα![]() sinβ)+
sinβ)+![]() ( cosα
( cosα![]() cosβ)=0,
cosβ)=0,
∴ 2sin![]() cos
cos![]() 2
2![]() sin
sin![]() sin
sin![]() ,
,
又sin![]() ≠0,
≠0,
∴ tan![]() ,
,
∴ 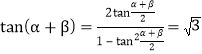 .
.

 阅读快车系列答案
阅读快车系列答案【题目】2020年初,新冠肺炎疫情袭击全国,某省由于人员流动性较大,成为湖北省外疫情最严重的省份之一,截至2月29日,该省已累计确诊1349例患者(无境外输入病例).
(1)为了解新冠肺炎的相关特征,研究人员从该省随机抽取100名确诊患者,统计他们的年龄数据,得下面的频数分布表:
年龄 |
|
|
|
|
|
|
|
|
|
人数 | 2 | 6 | 12 | 18 | 22 | 22 | 12 | 4 | 2 |
由频数分布表可以大致认为,该省新冠肺炎患者的年龄![]() 服从正态分布img src="https://thumb.zyjl.cn/questionBank/Upload/2020/05/25/11/70cd3e4c/SYS202005251112216152234742_ST/SYS202005251112216152234742_ST.011.png" width="80" height="22" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,其中
服从正态分布img src="https://thumb.zyjl.cn/questionBank/Upload/2020/05/25/11/70cd3e4c/SYS202005251112216152234742_ST/SYS202005251112216152234742_ST.011.png" width="80" height="22" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />,其中![]() 近似为这100名患者年龄的样本平均数(同一组中的数据用该组区间的中点值作代表).请估计该省新冠肺炎患者年龄在70岁以上(
近似为这100名患者年龄的样本平均数(同一组中的数据用该组区间的中点值作代表).请估计该省新冠肺炎患者年龄在70岁以上(![]() )的患者比例;
)的患者比例;
(2)截至2月29日,该省新冠肺炎的密切接触者(均已接受检测)中确诊患者约占10%,以这些密切接触者确诊的频率代替1名密切接触者确诊发生的概率,每名密切接触者是否确诊相互独立.现有密切接触者20人,为检测出所有患者,设计了如下方案:将这20名密切接触者随机地按![]() (
(![]() 且
且![]() 是20的约数)个人一组平均分组,并将同组的
是20的约数)个人一组平均分组,并将同组的![]() 个人每人抽取的一半血液混合在一起化验,若发现新冠病毒,则对该组的
个人每人抽取的一半血液混合在一起化验,若发现新冠病毒,则对该组的![]() 个人抽取的另一半血液逐一化验,记
个人抽取的另一半血液逐一化验,记![]() 个人中患者的人数为
个人中患者的人数为![]() ,以化验次数的期望值为决策依据,试确定使得20人的化验总次数最少的
,以化验次数的期望值为决策依据,试确定使得20人的化验总次数最少的![]() 的值.
的值.
参考数据:若![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.