题目内容
 (2012•虹口区二模)如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2,…,An,…,和点B1,B2,…,Bn…,其中A1
(2012•虹口区二模)如图,平面直角坐标系中,射线y=x(x≥0)和y=0(x≥0)上分别依次有点A1、A2,…,An,…,和点B1,B2,…,Bn…,其中A1
|
|
|
| 2 |
| 1 |
| 2 |
(1)用n表示|OAn|及点An的坐标;
(2)用n表示|BnBn+1|及点Bn的坐标;
(3)写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S(n),并求S(n)的最大值.
分析:(1)由|OAn|=|OA1|+(n-1)
=
•n,能求出An
.
(2)由|BnBn+1|=
|Bn-1Bn|=(
)n-1,知|OBn|=|OB1|+|B1B2|+…+|Bn-1Bn|=1+[1+
+…+(
)n-2]=3-(
)n-2,由此能用n表示|BnBn+1|及点Bn的坐标.
(3)由∠An+1OBn+1=
,写出四边形AnAn+1Bn+1Bn的面积关于n的表达式S(n),并求出S(n)的最大值.
| 2 |
| 2 |
|
(2)由|BnBn+1|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由∠An+1OBn+1=
| π |
| 4 |
解答:解:(1)∵|OAn|=|OA1|+(n-1)
=
•n…(2分)
∴An
…(4分)
(2)|BnBn+1|=
|Bn-1Bn|=(
)n-1…(7分)
|OBn|=|OB1|+|B1B2|+…+|Bn-1Bn|=1+[1+
+…+(
)n-2]=3-(
)n-2,
∴Bn
…(10分)
(3)∠An+1OBn+1=
,
∴
…(14分)
∵S(n)-S(n-1)=
,
∴n≥4时,S(n)单调递减.
又S(1)=
,S(2)=
=S(3)>S(4)=
.
∴n=2或3时,S(n)取得最大值
…(18分)
| 2 |
| 2 |
∴An
|
(2)|BnBn+1|=
| 1 |
| 2 |
| 1 |
| 2 |
|OBn|=|OB1|+|B1B2|+…+|Bn-1Bn|=1+[1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Bn
|
(3)∠An+1OBn+1=
| π |
| 4 |
∴
|
∵S(n)-S(n-1)=
| 3-n |
| 2n |
∴n≥4时,S(n)单调递减.
又S(1)=
| 3 |
| 2 |
| 7 |
| 4 |
| 27 |
| 16 |
∴n=2或3时,S(n)取得最大值
| 7 |
| 4 |
点评:本题考查数列与解析几何的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
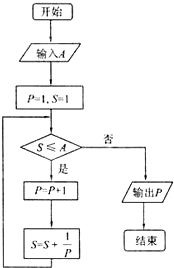 (2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为
(2012•虹口区二模)执行如图所示的程序框图,若输入A的值为2,则输出P的值为