题目内容
（2012•虹口区二模）a，b∈R，a＞b且ab=1，则
的最小值等于
| a2+b2 |
| a-b |
2
| 2 |
2
．| 2 |
分析：由a＞b且ab=1可得a-b＞0，则
=
=
=a-b+
，利用基本不等式可求最小值
| a2+b2 |
| a-b |
| (a-b)2+2ab |
| a-b |
| (a-b)2+2 |
| a-b |
| 2 |
| a-b |
解答：解：∵a＞b且ab=1
∴a-b＞0
∴
=
=
=a-b+
≥2
（当且仅当a-b=
即a-b=
时，取最小值2
）
故答案为：2
∴a-b＞0
∴
| a2+b2 |
| a-b |
| (a-b)2+2ab |
| a-b |
| (a-b)2+2 |
| a-b |
=a-b+
| 2 |
| a-b |
(a-b)•
|
（当且仅当a-b=
| 2 |
| a-b |
| 2 |
| 2 |
故答案为：2
| 2 |
点评：本题主要考查了基本不等式在求解最小值中的应用，解题的关键是配凑积为定值的变形．
练习册系列答案
阅读快车系列答案
相关题目
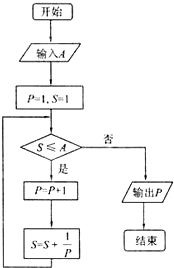（2012•虹口区二模）执行如图所示的程序框图，若输入A的值为2，则输出P的值为