Question

在平面直角坐标系中，O为坐标原点，设向

OA

=

a

，

OB

=

b

，其中

a

=(3，1)，

b

=(1，3)．若

OC

=λ

a

+μ

b

，0≤λ+μ≤1且λ，μ≥0，C点所有可能的位置区域的面积为

 

．

Answer 1

分析：设点C（x₀，y₀），根据已知等式若

OC

=λ

a

+μ

b

建立x₀、y₀的方程组，将其转化为λ+μ=

1

4

(x0+y0)，再根据0≤λ+μ≤1，且λ，μ≥0得出相应的不等式组，由不等式组作出符合题的平面区域，可以求出所要的区域的面积．

解答：解：设点C（x₀，y₀），因为

OC

=λ

a

+μ

b

，所以

x0=3λ+μ y0=λ+3μ

解之得：λ+μ=

1

4

(x0+y0)，λ=

3

8

x0-

1

8

y0且μ=-

1

8

x0+

3

8

y0
再由0≤λ+μ≤1，且λ，μ≥0
可得不等式组：

0≤ 1 4 (x0+y0)≤1 3 8 x0- 1 8 y0≥0 - 1 8 x0+ 3 8 y0≥ 0

，作出相应的平面区域如下图

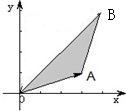
可得区域为△OAB，O（0，0），A（3，1），B（4，4）
因此可以算出△OAB的面积为：S=

1

2

×(4×4) -

1

2

×3×1-

1

2

×1×3-1×1=4
故答案为：4

点评：本题主要考查了两个知识点：平面向量的坐标运算以及一元二次不等式组所表示的平面区域，同时考查了阅读理解题意的能力以及简单的转化思想和数形结合的思想，属中档题．