题目内容
设sin(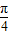 +θ)=
+θ)= ,则sin2θ=( )
,则sin2θ=( )A.-

B.-

C.

D.

【答案】分析:根据两角和的正弦函数公式和特殊角的三角函数值化简已知条件,然后两边平方利用同角三角函数间的基本关系及二倍角的正弦函数公式化简,即可sin2θ的值.
解答:解:由sin(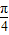 +θ)=sin
+θ)=sin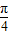 cosθ+cos
cosθ+cos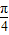 sinθ=
sinθ=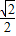 (sinθ+cosθ)=
(sinθ+cosθ)= ,
,
两边平方得:1+2sinθcosθ= ,即2sinθcosθ=-
,即2sinθcosθ=- ,
,
则sin2θ=2sinθcosθ=- .
.
故选A
点评:此题考查学生灵活运用二倍角的正弦函数公式、两角和与差的正弦函数公式及特殊角的三角函数值化简求值,是一道基础题.
解答:解:由sin(
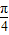 +θ)=sin
+θ)=sin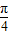 cosθ+cos
cosθ+cos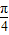 sinθ=
sinθ=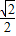 (sinθ+cosθ)=
(sinθ+cosθ)= ,
,两边平方得:1+2sinθcosθ=
 ,即2sinθcosθ=-
,即2sinθcosθ=- ,
,则sin2θ=2sinθcosθ=-
 .
.故选A
点评:此题考查学生灵活运用二倍角的正弦函数公式、两角和与差的正弦函数公式及特殊角的三角函数值化简求值,是一道基础题.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
 如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是
如图所示,ABCD是一块边长为7米的正方形铁皮,其中ATN是一半径为6米的扇形,已经被腐蚀不能使用,其余部分完好可利用.工人师傅想在未被腐蚀部分截下一个有边落在BC与CD上的长方形铁皮PQCR,其中P是