题目内容
设 ,曲线
,曲线 在点
在点 处的切线与直线
处的切线与直线 垂直.
垂直.
(1)求 的值;
的值;
(2)若对于任意的 ,
, 恒成立,求
恒成立,求 的范围;
的范围;
(3)求证: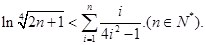
解析试题分析:(1)求得函数f(x)的导函数,利用曲线y=f(x)在点(1,f(1))处的切线与直线2x+y+1=0垂直,即可求a的值;
(2)先将原来的恒成立问题转化为lnx≤m(x?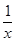 ),设g(x)=lnx?m(x?
),设g(x)=lnx?m(x?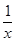 ),即?x∈(1,+∞),g(x)≤0.利用导数研究g(x)在(0,+∞)上单调性,求出函数的最大值,即可求得实数m的取值范围.
),即?x∈(1,+∞),g(x)≤0.利用导数研究g(x)在(0,+∞)上单调性,求出函数的最大值,即可求得实数m的取值范围.
(3)由(2)知,当x>1时,m=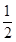 时,lnx<
时,lnx<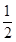 (x?
(x?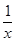 )成立.不妨令x=
)成立.不妨令x=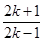 ,k∈N*,得出
,k∈N*,得出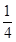 [ln(2k+1)?ln(2k?1)]<
[ln(2k+1)?ln(2k?1)]<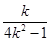 ,k∈N*,再分别令k=1,2,,n.得到n个不等式,最后累加可得.
,k∈N*,再分别令k=1,2,,n.得到n个不等式,最后累加可得.
(1)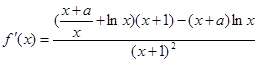 2分
2分
由题设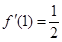 ,∴
,∴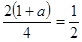
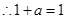 ,
,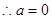 . 4分
. 4分
(2)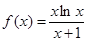 ,
,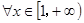 ,
,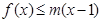 ,即
,即
设 ,即
,即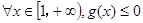 .
. 6分
6分
①若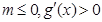 ,
,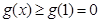 ,这与题设
,这与题设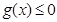 矛盾. 7分
矛盾. 7分
②若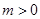 方程
方程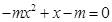 的判别式
的判别式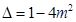
当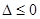 ,即
,即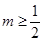 时,
时,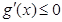 .
. 在
在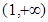 上单调递减,
上单调递减,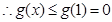 ,即不等式成立. 8分
,即不等式成立. 8分
当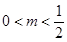 时,方程
时,方程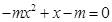 ,设两根为
,设两根为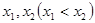
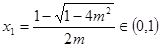 ,
,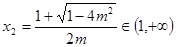
当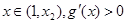 ,
,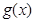 单调递增,
单调递增,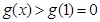 ,与题设矛盾.
,与题设矛盾.
综上所述,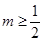 . 10分
. 10分
(3) 由(2)知,当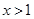 时,
时, 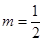 时,
时,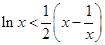 成立.
成立.
不妨令
所以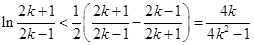 ,
,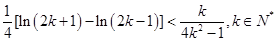 11分
11分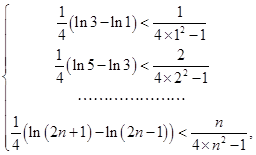 12分
12分
累加可得
∴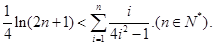
∴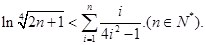 ---------------14分
---------------14分
考点:1.利用导数研究曲线上某点切线方程;2.导数在最大值、最小值问题中的应用.

练习册系列答案
相关题目
 ,-
,- ]上有单调递增区间?
]上有单调递增区间? (
( )
) 时,求函数
时,求函数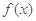 的极值;(2)当
的极值;(2)当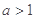 时,讨论
时,讨论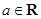 ,函数
,函数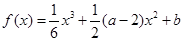 ,
,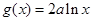 .
.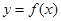 与曲线
与曲线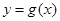 在它们的交点
在它们的交点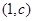 处的切线互相垂直,求
处的切线互相垂直,求 ,
,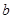 的值;
的值;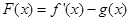 ,若对任意的
,若对任意的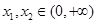 ,且
,且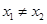 ,都有
,都有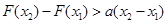 ,求
,求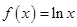 ,
,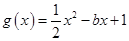 (
(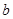 为常数).
为常数).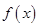 的图象在点
的图象在点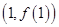 处的切线与函数
处的切线与函数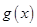 的图象相切,求实数
的图象相切,求实数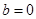 ,
,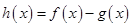 ,
,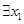 、
、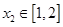 使得
使得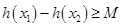 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数 ;
;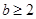 时,若对于区间
时,若对于区间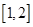 内的任意两个不相等的实数
内的任意两个不相等的实数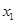 、
、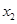 ,都有
,都有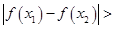
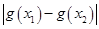 成立,求
成立,求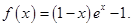
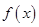 的最大值;
的最大值;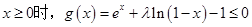 ,求
,求 的取值范围.
的取值范围.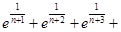 +
+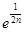
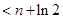 (n
(n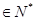 )
)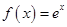 .
.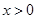 时,设
时,设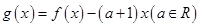 .讨论函数
.讨论函数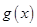 的单调性;
的单调性;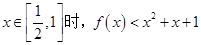 .
.