题目内容
等差数列{an}中,Sn是它的前n项和,若S16>0,且S17<0,则当Sn最大时n的值为 .
考点:等差数列的性质
专题:等差数列与等比数列
分析:由题意和等差数列的前n项和公式得
,利用等差数列的性质可得
,从而判断出数列的单调性以及正负项对应的n的范围,再求出当Sn最大时n的值.
|
|
解答:
解:由题意得,S16>0,且S17<0,
所以
,则
,
由等差数列的性质得,a9+a8>0,所以
,
所以等差数列{an}是递减数列,前八项大于零,从第九项起都小于零,
所以当Sn最大时n的值为8,
故答案为:8.
所以
|
|
由等差数列的性质得,a9+a8>0,所以
|
所以等差数列{an}是递减数列,前八项大于零,从第九项起都小于零,
所以当Sn最大时n的值为8,
故答案为:8.
点评:本题考查等差数列的前n项和公式、性质的灵活应用,以及利用等差数列的单调性求出当Sn最大时n的值.

练习册系列答案
相关题目
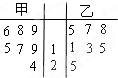 某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲运动员得分的中位数,乙运动员的平均数分别为( )
某赛季,甲、乙两名篮球运动员都参加了7场比赛,他们所有比赛得分的情况用如图所示的茎叶图表示,则甲运动员得分的中位数,乙运动员的平均数分别为( )| A、15、12 |
| B、15、15 |
| C、19、11 |
| D、19、15 |
log29×log34=( )
A、
| ||
| B、4 | ||
| C、2 | ||
D、
|
在等差数列{an}中,设公差d=1,a2是a1与a4的等比中项,则a1=( )
| A、2 | B、1 | C、2或1 | D、1或-1 |