题目内容
已知抛物线C:y2=4x,F是C的焦点,过焦点F的直线l与C交于 A,B两点,O为坐标原点.(1)求
 •
• 的值;
的值;(2)设
 =λ•
=λ• ,求△ABO的面积S的最小值;
,求△ABO的面积S的最小值;(3)在(2)的条件下若S≤
 ,求λ的取值范围.
,求λ的取值范围.
【答案】分析:(1)可设l的方程x=my+1,将其与C的方程联立,消去x可得y2-4my-4=0.设A、B点的坐标分别为(x1,y1),(x2,y2)(y1>0>y2),由根与系数关系可得x1x2和y1y2的值,代入数量积公式可得; (2)由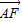 =λ•
=λ•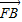 ,计算可得y2=-
,计算可得y2=-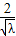 ,y1=2
,y1=2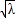 ,代入可得S=
,代入可得S= |OF|•|y1-y2|=
|OF|•|y1-y2|=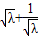 ,由基本不等式可得;(3)可得
,由基本不等式可得;(3)可得 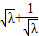 ≤
≤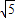 解之即可.
解之即可.
解答:解:(1)根据抛物线的方程可得焦点F(1,0),设直线l的方程为x=my+1,
将其与C的方程联立,消去x可得y2-4my-4=0.
设A、B点的坐标分别为(x1,y1),(x2,y2)(y1>0>y2),则y1y2=-4.
因为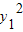 =4x1,
=4x1,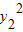 =4x2,所以x1x2=
=4x2,所以x1x2=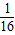
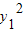
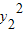 =1,
=1,
故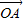 •
•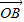 =x1x2+y1y2=-3 …(4分)
=x1x2+y1y2=-3 …(4分)
(2)因为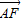 =λ•
=λ•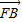 ,所以(1-x1,-y1)=λ(x2-1,y2),
,所以(1-x1,-y1)=λ(x2-1,y2),
即 1-x1=λx2-λ①-y1=λy2②
又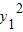 =4x1 ③,
=4x1 ③,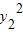 =4x2,④,由②③④消去y1,y2后,得到x1=λ2x2,将其代入①,
=4x2,④,由②③④消去y1,y2后,得到x1=λ2x2,将其代入①,
注意到λ>0,解得x2= .从而可得y2=-
.从而可得y2=-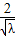 ,y1=2
,y1=2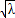 ,故△OAB的面积S=
,故△OAB的面积S= |OF|•|y1-y2|=
|OF|•|y1-y2|=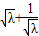
因为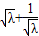 ≧2恒成立,故△OAB的面积S的最小值是2…(8分).
≧2恒成立,故△OAB的面积S的最小值是2…(8分).
(3)由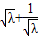 ≤
≤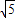 解之得
解之得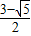 ≤λ≤
≤λ≤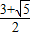 …(12分)
…(12分)
点评:本题考查平面向量数量积的运算,涉及圆锥曲线和基本不等式的应用,属中档题.
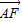 =λ•
=λ•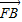 ,计算可得y2=-
,计算可得y2=-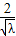 ,y1=2
,y1=2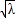 ,代入可得S=
,代入可得S= |OF|•|y1-y2|=
|OF|•|y1-y2|=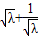 ,由基本不等式可得;(3)可得
,由基本不等式可得;(3)可得 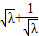 ≤
≤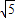 解之即可.
解之即可.解答:解:(1)根据抛物线的方程可得焦点F(1,0),设直线l的方程为x=my+1,
将其与C的方程联立,消去x可得y2-4my-4=0.
设A、B点的坐标分别为(x1,y1),(x2,y2)(y1>0>y2),则y1y2=-4.
因为
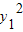 =4x1,
=4x1,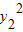 =4x2,所以x1x2=
=4x2,所以x1x2=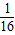
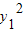
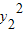 =1,
=1,故
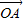 •
•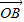 =x1x2+y1y2=-3 …(4分)
=x1x2+y1y2=-3 …(4分)(2)因为
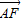 =λ•
=λ•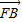 ,所以(1-x1,-y1)=λ(x2-1,y2),
,所以(1-x1,-y1)=λ(x2-1,y2),即 1-x1=λx2-λ①-y1=λy2②
又
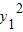 =4x1 ③,
=4x1 ③,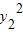 =4x2,④,由②③④消去y1,y2后,得到x1=λ2x2,将其代入①,
=4x2,④,由②③④消去y1,y2后,得到x1=λ2x2,将其代入①,注意到λ>0,解得x2=
 .从而可得y2=-
.从而可得y2=-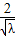 ,y1=2
,y1=2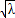 ,故△OAB的面积S=
,故△OAB的面积S= |OF|•|y1-y2|=
|OF|•|y1-y2|=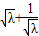
因为
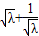 ≧2恒成立,故△OAB的面积S的最小值是2…(8分).
≧2恒成立,故△OAB的面积S的最小值是2…(8分).(3)由
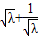 ≤
≤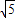 解之得
解之得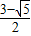 ≤λ≤
≤λ≤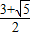 …(12分)
…(12分)点评:本题考查平面向量数量积的运算,涉及圆锥曲线和基本不等式的应用,属中档题.

练习册系列答案
相关题目
 如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点).
如图,已知抛物线C:y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4且位于x轴上方的点. A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M(O为坐标原点). 已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.
已知抛物线C:y2=4x,点M(m,0)在x轴的正半轴上,过M的直线l与C相交于A、B两点,O为坐标原点.