题目内容
如图,直三棱柱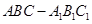 中,点
中,点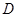 是
是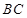 上一点.
上一点.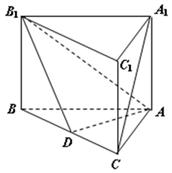
⑴若点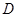 是
是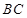 的中点,求证
的中点,求证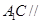 平面
平面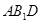 ;
;
⑵若平面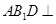 平面
平面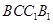 ,求证
,求证 .
.
(1)详见解析,(2)详见解析.
解析试题分析:(1)要证线面平行,需有线线平行.由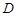 为
为 的中点,想到取
的中点,想到取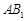 的中点
的中点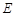 ;证
;证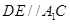 就成为解题方向,这可利用三角形中位线性质来证明.在由线线平行证线面平行时,需完整表示定理条件,尤其是线在面外这一条件;(2)证明线线垂直,常利用线面垂直.由直三棱柱性质易得底面
就成为解题方向,这可利用三角形中位线性质来证明.在由线线平行证线面平行时,需完整表示定理条件,尤其是线在面外这一条件;(2)证明线线垂直,常利用线面垂直.由直三棱柱性质易得底面 直线
直线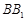 ,所以有
,所以有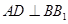 ,因而需在侧面
,因而需在侧面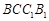 再找一直线与直线
再找一直线与直线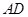 垂直. 利用平面
垂直. 利用平面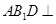 平面
平面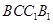 可实现这一目标. 过
可实现这一目标. 过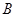 作
作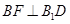 ,由面面垂直性质定理得
,由面面垂直性质定理得 侧面
侧面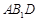 ,从而有
,从而有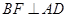 ,因此有线面垂直:
,因此有线面垂直: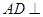 面
面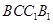 ,因此
,因此 .在面面垂直与线面垂直的转化过程中,要注意列全定理所需要的所有条件.
.在面面垂直与线面垂直的转化过程中,要注意列全定理所需要的所有条件.
试题解析: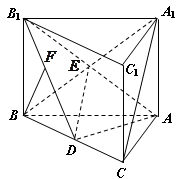
(1)连接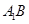 ,设
,设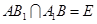 ,则
,则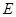 为
为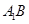 的中点, 2分
的中点, 2分
连接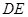 ,由
,由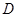 是
是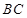 的中点,得
的中点,得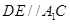 , 4分
, 4分
又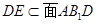 ,且
,且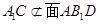 ,
,
所以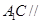 平面
平面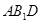 7分
7分
⑵在平面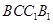 中过
中过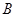 作
作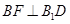 ,因平面
,因平面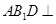 平面
平面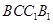 ,
,
又平面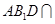 平面
平面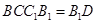 ,所以
,所以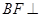 平面
平面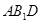 , 10分
, 10分
所以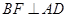 ,
,
在直三棱柱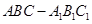 中,
中,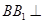 平面
平面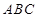 ,所以
,所以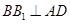 , 12分
, 12分
又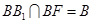 ,所以
,所以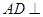 平面
平面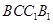 ,所以
,所以 . 15分
. 15分
考点:线面平行判定定理,线线垂直判定定理,

练习册系列答案
相关题目
 BC.
BC.

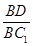 的值.
的值.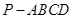 中,底面
中,底面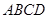 是平行四边形,
是平行四边形,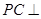 平面
平面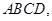
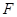 是
是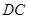 的中点,
的中点,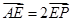 .
.
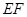 与平面
与平面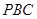 的位置关系,并予以证明;
的位置关系,并予以证明;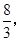
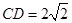 ,
,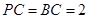 ,求证:平面
,求证:平面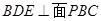 .
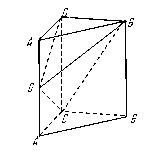
.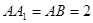 .
.
 与平面
与平面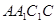 所成角的正弦值;
所成角的正弦值;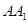 上是否存在点
上是否存在点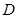 ?使得二面角
?使得二面角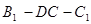 的大小为60°,若存在,求出
的大小为60°,若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.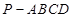 中,
中,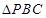 为正三角形,
为正三角形,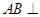 平面
平面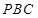 ,
,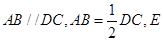 为
为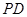 的中点.
的中点.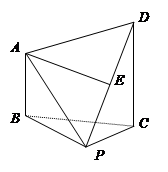
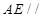 平面
平面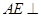 平面
平面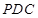 .
. 所在的平面与正方形
所在的平面与正方形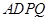 所在的平面相互垂直,
所在的平面相互垂直,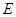 是
是 的中点.
的中点.
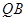 ∥平面
∥平面 ;
; ⊥平面
⊥平面 是正方形,
是正方形, 平面
平面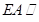
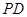 ,
,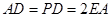 ,
,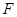 ,
,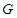 ,
, 分别为
分别为 ,
,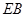 ,
, 的中点.
的中点.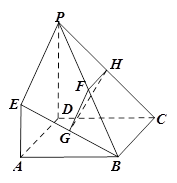
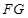
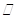 平面
平面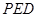 ;
;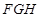 与平面
与平面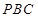 所成锐二面角的大小.
所成锐二面角的大小.