题目内容
(1)求抛物线y2=x与直线x-2y-3=0所围成的图形的面积.
(2)求下列定积分
(2sinx+cosx)dx.
(2)求下列定积分
| ∫ |
0 |
分析:(1)先计算抛物线y2=x和直线x-2y-3=0的交点纵坐标,确定积分上下限,再由定积分的几何意义,将图形面积问题转化为上下两函数差的定积分问题,最后利用微积分基本定理求值即可
(2)利用积分基本定理,先求出被积函数,然后即可求解
(2)利用积分基本定理,先求出被积函数,然后即可求解
解答: 解:(1)由
解:(1)由
可得A(1,-1),B(9,3)
∴S=
[
-(-
)]dx
[
-
(x-3)]dx=
(2)
(2sinx+cosx)dx=2
sinxdx
cosxdx
=-2cosx
+sinx
=-2(0-1)+(1-0)=3
 解:(1)由
解:(1)由
|
∴S=
| ∫ | 1 0 |
| x |
| x |
| +∫ | 9 1 |
| x |
| 1 |
| 2 |
| 32 |
| 3 |
(2)
| ∫ |
0 |
| ∫ |
0 |
| +∫ |
0 |
=-2cosx
| | |
0 |
| | |
0 |
=-2(0-1)+(1-0)=3
点评:本题主要考查了积分的求解,解题的关键是积分基本定理及积分的几何意义的应用

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 设抛物线M方程为y2=2px(p>0),其焦点为F,P(a,b)(a≠0)为直线y=x与抛物线M的一个交点,|PF|=5
设抛物线M方程为y2=2px(p>0),其焦点为F,P(a,b)(a≠0)为直线y=x与抛物线M的一个交点,|PF|=5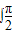 (2sinx+cosx)dx.
(2sinx+cosx)dx.