题目内容
直线y=x+b与曲线y=
有且只有一个公共点,则b的取值范围是( )
| 4-x2 |
分析:曲线y=
表示一个半圆,当直线y=x+b与半圆相切时,求得b的值;当直线y=x+b过点(-2,0)时,求得b的值;当直线y=x+b过点(2,0)时,求得b的值,数形结合可得b的范围.
| 4-x2 |
解答: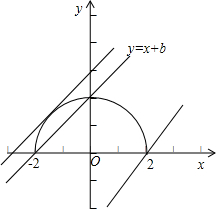 解:曲线y=
解:曲线y=
即 x2+y2=4 (y≥0),
表示以原点为圆心,半径等于2的半圆,如图.
当直线y=x+b与半圆相切时,由2=
,可得 b=2
,或b=-2
(舍去).
当直线y=x+b过点(-2,0),
把点(-2,0)代入直线y=x+b可得0=-2+b,故b=2.
当直线y=x+b过点(2,0),
把点(2,0)代入直线y=x+b可得,0=2+b,故b=-2.
数形结合可得,当直线y=x+b与曲线y=
有且只有
一个公共点时,
则b的取值范围是-2≤b<2,或b=2
,
故选 C.
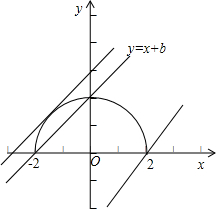 解:曲线y=
解:曲线y=| 4-x2 |
表示以原点为圆心,半径等于2的半圆,如图.
当直线y=x+b与半圆相切时,由2=
| |0-0+b| | ||
|
| 2 |
| 2 |
当直线y=x+b过点(-2,0),
把点(-2,0)代入直线y=x+b可得0=-2+b,故b=2.
当直线y=x+b过点(2,0),
把点(2,0)代入直线y=x+b可得,0=2+b,故b=-2.
数形结合可得,当直线y=x+b与曲线y=
| 4-x2 |
一个公共点时,
则b的取值范围是-2≤b<2,或b=2
| 2 |
故选 C.
点评:本题主要函数的零点的定义,体现了数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
若直线y=x-b与曲线
(θ∈[0,2π))有两个不同的公共点,则实数b的取值范围为( ).
|
A、(2-
| ||||
B、[2-
| ||||
C、(-∞,2-
| ||||
D、(2-
|
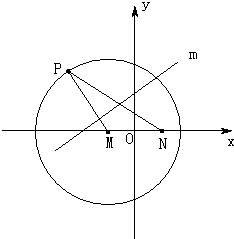 如图,已知
如图,已知