题目内容
已知椭圆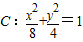
的左焦点为F1，直线l：y=x-2与椭圆C交于A、B两点．（1）求线段AB的长；
（2）求△ABF1的面积．
【答案】分析：（1）把直线方程代入椭圆方程，求得交点坐标，可求线段AB的长；
（2）法一：求出点F1（-2，0）到直线y=x-2的距离，可求△ABF1的面积；法二：直线y=x-2通过椭圆的右焦点，利用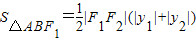
，可得结论．
解答：解：（1）设A（x1，y1），B（x2，y2）．
因为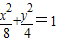
和y=x-2相交，把两个方程联立，得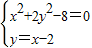
代入得到x2+2（x-2）2-8=0，即3x2-8x=0，解得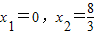
所以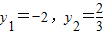
，
所以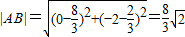
（2）法一：因为点F1（-2，0）到直线y=x-2的距离为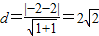
所以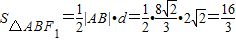
法二：直线y=x-2通过椭圆的右焦点F2（2，0），
则△ABF2的面积为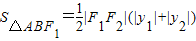
=
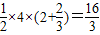
点评：本题考查直线与椭圆的位置关系，考查三角形面积的计算，考查学生的计算能力，属于中档题．
（2）法一：求出点F1（-2，0）到直线y=x-2的距离，可求△ABF1的面积；法二：直线y=x-2通过椭圆的右焦点，利用
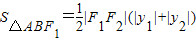，可得结论．解答：解：（1）设A（x1，y1），B（x2，y2）．
因为
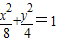和y=x-2相交，把两个方程联立，得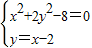代入得到x2+2（x-2）2-8=0，即3x2-8x=0，解得
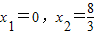
所以
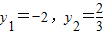，所以
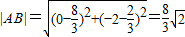
（2）法一：因为点F1（-2，0）到直线y=x-2的距离为
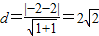
所以
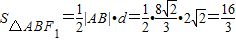
法二：直线y=x-2通过椭圆的右焦点F2（2，0），
则△ABF2的面积为
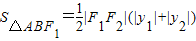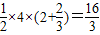
=点评：本题考查直线与椭圆的位置关系，考查三角形面积的计算，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
的左焦点为F，O为坐标原点。
相切的圆的方程；
轴交于点G，求点G横坐标的取值范围。
的左焦点为F，O为坐标原点．
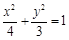的左焦点为F，过点F的直线交椭圆于A、B两点，线段AB的中点为G，AB的中垂线与x轴和y轴分别交于D、E两点．
，求直线AB的斜率；
的左焦点为F，左右顶点分别为A、C，
，其中圆心P的坐标为
．
，求
上，求椭圆的方程．
的左焦点为F，右顶点为A，点B在椭圆上，且
轴，直线AB交
轴于点P。若
，则椭圆的离心率为