题目内容
长度为a(a>0)的线段AB的两个端点A、B分别在x轴和y轴上滑动,点P在线段AB上,且满足(1)求点P的轨迹方程C;
(2)当a=λ+1时,过点M(1,0)作两条互相垂直的直线l1和l2,l1和l2分别与曲线C相交于点N和Q(都异于点M),试问△MNQ能不能是等腰三角形?若能,这样的三角形有几个;若不能,请说明理由.
解:(1)依题意,设点A,B的坐标分别为(x1,0),(0,y1),点P的坐标为(x,y).
由![]() =λ
=λ![]() ,故(x-x1,y)=λ(-x,y1-y)=(-λx,λ(y1-y)).
,故(x-x1,y)=λ(-x,y1-y)=(-λx,λ(y1-y)).
∴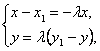 即
即
∵|AB|=a,∴x![]() +y
+y![]() =a2.∴(1+λ)2x2+(
=a2.∴(1+λ)2x2+(![]() )2y2= a2
)2y2= a2
∴点P的轨迹方程C是(1+λ)2x2+(![]() )2y2=a2.
)2y2=a2.
(2)当a=λ+1时,曲线C的方程是x2+![]() =1,故点M(1,0)在曲线C上.
=1,故点M(1,0)在曲线C上.
依题意,可知直线l1和l2都不可能与坐标轴平行,
可设直线l1方程为y=k(x-1),直线l2方程为y=-![]() (x-1),不妨设k>0.
(x-1),不妨设k>0.
由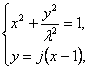 消去y得(λ2+k2)x2-2k2x+k2-λ2=0.
消去y得(λ2+k2)x2-2k2x+k2-λ2=0.
由xm·xn=![]() ,又xm=1,得xn=
,又xm=1,得xn=![]() ,
,
∴|MN|=![]() |xn-xm|=
|xn-xm|=![]() |
|![]() -1|=
-1|=![]() ·
·![]() .
.
同理可得|MQ|=![]() ·
·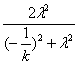 =
=![]() ·
·![]() .
.
假设ΔMNQ是等腰三角形,则|MN|=|MQ|,即![]() ·
·![]() =
=![]() ·
·![]() ,
,
化简得(k-1)[k2+(1-λ2)k+1]=0,
∴k=1或k2+(1-λ2)k+1=0. ①
①式的叛别式Δ=(1-λ2)2-4,
在RTΔEBD′中,![]() =
=![]() ,可求得FG=
,可求得FG=![]() .
.
∴sin∠FAG=![]() =
=![]() =
=![]() .
.
∴直线AC与平面ABD′所成的角为Arcsin![]() .
.

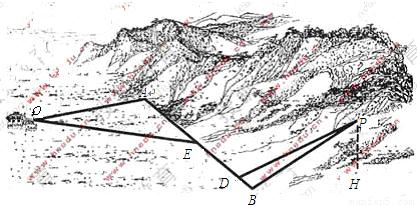
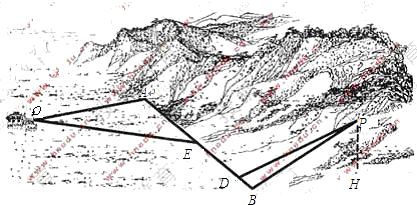
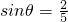 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为 万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km),
万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km),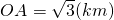 .
.
 ,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为
,点P到平面α的距离PH=0.4(km).沿山脚原有一段笔直的公路AB可供利用、从点O到山脚修路的造价为a万元/km,原有公路改建费用为 万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km),
万元/km、当山坡上公路长度为lkm(1≤l≤2)时,其造价为(l2+1)a万元、已知OA⊥AB,PB⊥AB,AB=1.5(km), .
.