题目内容
下列四个命题:①若 ,则
,则 ; ②若△ABC不是直角三角形,则tanAtanBtanC=tanA+tanB+tanC;③函数
; ②若△ABC不是直角三角形,则tanAtanBtanC=tanA+tanB+tanC;③函数 的最小正周期为2π;④
的最小正周期为2π;④ .其中正确的命题为________.(写出所有正确命题的序号)
.其中正确的命题为________.(写出所有正确命题的序号)
②③④
分析:这是一道关于向量与三角函数知识的判断题,因此根据相关知识逐个加以判断.根据向量的运算法则,可得命题①不正确而命题④正确,根据三角函数和的正切公式推导可得命题②正确,根据正切函数的周期规律,得出命题③正确.
解答:对各个选项分别加以判别:
对于①,若 ,移项得
,移项得 ,
,
说明向量 与向量
与向量 互相垂直,不一定有
互相垂直,不一定有 ,故①不正确;
,故①不正确;
对于②,若△ABC不是直角三角形,则由tan(B+C)=tan(π-A),得
 ,
,
整理可得tanAtanBtanC=tanA+tanB+tanC,故②正确;
对于③,根据正切函数周期公式可得y=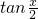 的周期为2π,
的周期为2π,
再取绝对值,得函数 的最小正周期为2π,命题③正确;
的最小正周期为2π,命题③正确;
对④, =
= -
- =1-1=0,命题④正确;
=1-1=0,命题④正确;
故答案为:②③④
点评:本题以三角函数与向量的有关知识为载体,考查了命题真假的判断,属于中档题.
分析:这是一道关于向量与三角函数知识的判断题,因此根据相关知识逐个加以判断.根据向量的运算法则,可得命题①不正确而命题④正确,根据三角函数和的正切公式推导可得命题②正确,根据正切函数的周期规律,得出命题③正确.
解答:对各个选项分别加以判别:
对于①,若
 ,移项得
,移项得 ,
,说明向量
 与向量
与向量 互相垂直,不一定有
互相垂直,不一定有 ,故①不正确;
,故①不正确;对于②,若△ABC不是直角三角形,则由tan(B+C)=tan(π-A),得
 ,
,整理可得tanAtanBtanC=tanA+tanB+tanC,故②正确;
对于③,根据正切函数周期公式可得y=
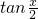 的周期为2π,
的周期为2π,再取绝对值,得函数
 的最小正周期为2π,命题③正确;
的最小正周期为2π,命题③正确;对④,
 =
= -
- =1-1=0,命题④正确;
=1-1=0,命题④正确;故答案为:②③④
点评:本题以三角函数与向量的有关知识为载体,考查了命题真假的判断,属于中档题.

练习册系列答案
相关题目
 则
则 ;②。若
;②。若 则
则 ;
; ,则
,则 ; ④。若
; ④。若 ,则
,则 、
、 .下列四个命题中,
.下列四个命题中,

