题目内容
【题目】已知函数![]() ,其中
,其中![]() ,
,![]() .
.
(1)若![]() ,
,![]() ,且对任意的
,且对任意的![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(2)若![]() ,
,![]() ,且
,且![]() 在
在![]() 单调递增,求
单调递增,求![]() 的最大值.
的最大值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)代入![]() ,
,![]() 可求得
可求得![]() 的解析式.代入不等式化简,将不等式化简为关于
的解析式.代入不等式化简,将不等式化简为关于![]() 的二次函数形式,结合
的二次函数形式,结合![]() 即可求得
即可求得![]() 的取值范围.
的取值范围.
(2)解法1:根据条件![]() 可求得函数
可求得函数![]() 的对称轴,且由
的对称轴,且由![]() 可得
可得![]() 的表达式.再根据
的表达式.再根据![]() 在
在![]() 单调递增,可得关于
单调递增,可得关于![]() 的不等式组,解不等式组即可求得
的不等式组,解不等式组即可求得![]() 的最大值.
的最大值.
解法2:根据![]() 在
在![]() 单调递增可先求得
单调递增可先求得![]() 的取值范围,结合
的取值范围,结合![]() 可得函数
可得函数![]() 的对称轴, 且由
的对称轴, 且由![]() 可得
可得![]() 的表达式.根据
的表达式.根据![]() 可求得
可求得![]() 的值,再求得于
的值,再求得于![]() 的值,即可得
的值,即可得![]() 的解析式.进而求得满足
的解析式.进而求得满足![]() 在
在![]() 单调递增时
单调递增时![]() 的最大值.
的最大值.
(1)∵![]() ,
,![]()
∴![]()
![]()
![]()
![]()
∴![]() ,即
,即![]()
![]()
∵![]()
∴![]()
∴当![]() 时,
时,![]()
∴![]()
(2)解法1:∵![]()
∴![]() 为
为![]() 图像的对称轴
图像的对称轴
又![]()
∴
两式相减得![]()
∴![]()
∵![]() 在
在![]() 单调递增,令
单调递增,令![]()
∴![]() 在
在![]() 单调递增
单调递增
∴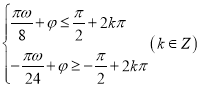 ,则
,则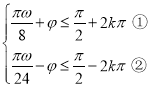 ,
,
①+②得![]()
∴![]()
∵![]()
∴当![]() 时
时![]() 取到最大值为
取到最大值为![]()
解法2:![]() 在
在![]() 单调递增
单调递增
∴![]()
∴![]()
∵![]()
∴![]() 为
为![]() 图像的对称轴
图像的对称轴
又![]()
∴
两式相加得![]()
∵![]()
∴![]() 或
或![]()
①当![]() 时,
时,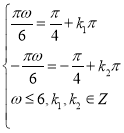 ,得
,得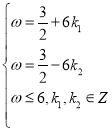 ,
,![]()
②当![]() 时
时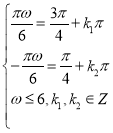 ,得
,得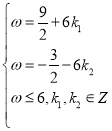 ,
,![]()
当![]() ,
,![]() 时
时![]()
![]() 时,
时,![]()
则满足条件![]() 在
在![]() 单调递增,所以
单调递增,所以![]() 的最大值为
的最大值为![]() .
.

练习册系列答案
相关题目