题目内容
若函数f(x)＝kax－a－x(a＞0且a≠1)在(－∞，＋∞)上既是奇函数又是增函数，则函数g(x)＝loga(x＋k)的图象是
[ ]
A．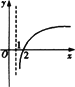
B．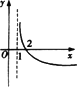
C．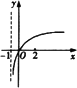
D．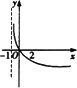
答案：C
练习册系列答案
小学课时特训系列答案
相关题目
小学课时特训系列答案题目内容
若函数f(x)＝kax－a－x(a＞0且a≠1)在(－∞，＋∞)上既是奇函数又是增函数，则函数g(x)＝loga(x＋k)的图象是
A．
B．
C．
D．
小学课时特训系列答案
，－1)，b＝(
，
)．
，－1)，b＝(
，
)，若存在不同时为0的实数k和t，使得x＝a＋(t2－3)b，y＝－ka＋tb，且x⊥y，试确定函数k＝f(t)的单调区间．
，－1)，b＝
.
，－1)，b＝(
, 
).