题目内容
已知平面向量a=(![]() ,-1),b=(
,-1),b=(![]() ,
, ![]() ).
).
(1) 若存在实数k和t,便得x=a+(t2-3)b, y=-ka+tb,且x⊥y,试求函数的关系式k=f(t);
(2) 根据(1)的结论,确定k=f(t)的单调区间。
分析:利用向量知识转化为函数问题求解.
解:(1)法一:由题意知x=(![]() ,
,![]() ),
),
y=(![]()
![]() t-
t-![]() k,
k,![]() t+k),又x⊥y
t+k),又x⊥y
故x · y=![]() ×(
×(![]() t-
t-![]() k)+
k)+![]() ×(
×(![]() t+k)=0。
t+k)=0。
整理得:t3-3t-4k=0,即k=![]() t3-
t3-![]() t.
t.
法二:∵a![]() =(
=(![]() ,-1),b=(
,-1),b=(![]() ,
, ![]() ), ∴.
), ∴. ![]() =2,
=2,![]() =1且a⊥b
=1且a⊥b
∵x⊥y,∴x · y=0,即-k![]() 2+t(t2-3)
2+t(t2-3)![]() 2=0,∴t3-3t-4k=0,即k=
2=0,∴t3-3t-4k=0,即k=![]() t3-
t3-![]() t
t
(2) 由(1)知:k=f(t) =![]() t3-
t3-![]() t ∴k´=f´(t) =
t ∴k´=f´(t) =![]() t2-
t2-![]() ,
,
令k´<0得-1<t<1;令k´>0得t<-1或t>1.
故k=f(t)的单调递减区间是(-1, 1 ),单调递增区间是(-∞,-1)和(1,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
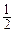 a-
a- b= .
b= .