题目内容
设向量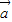 =(4cosα,sinα),
=(4cosα,sinα),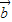 =(sinβ,4cosβ),
=(sinβ,4cosβ),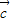 =(cosβ,4sinβ)
=(cosβ,4sinβ)(1)若
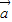 与
与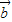 -2
-2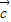 垂直,求tan(α+β)的值;
垂直,求tan(α+β)的值;(2)求|
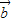 +
+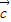 |的最大值.
|的最大值.
【答案】分析:(1)根据向量的数乘运算及向量坐标的减法运算求出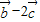 ,然后由向量垂直的条件得到关于α,β的三角函数关系式,整理后即可得到tan(α+β)的值;
,然后由向量垂直的条件得到关于α,β的三角函数关系式,整理后即可得到tan(α+β)的值;
(2)写出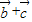 ,然后直接运用求模公式求出模,运用三角函数的有关公式化简后即可求模的最大值.
,然后直接运用求模公式求出模,运用三角函数的有关公式化简后即可求模的最大值.
解答:解:(1)∵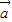 =(4cosα,sinα),
=(4cosα,sinα),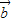 =(sinβ,4cosβ),由
=(sinβ,4cosβ),由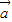 与
与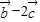 垂直,∴
垂直,∴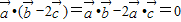 ,
,
即4sin(α+β)-8cos(α+β)=0,∴tan(α+β)=2;
(2)∵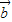 =(sinβ,4cosβ),
=(sinβ,4cosβ),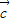 =(cosβ,4sinβ)
=(cosβ,4sinβ)
则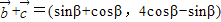 ,
,
∴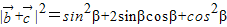 +16cos2β-32cosβsinβ+16sin2β
+16cos2β-32cosβsinβ+16sin2β
=17-30sinβcosβ=17-15sin2β,最大值为32,所以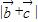 的最大值为4
的最大值为4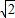 .
.
点评:本题考查了运用数量积判断两个向量的垂直关系,考查了向量的模,考查了同角三角函数间的基本关系式,考查了学生的运算能力,此题是基础题.
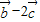 ,然后由向量垂直的条件得到关于α,β的三角函数关系式,整理后即可得到tan(α+β)的值;
,然后由向量垂直的条件得到关于α,β的三角函数关系式,整理后即可得到tan(α+β)的值;(2)写出
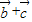 ,然后直接运用求模公式求出模,运用三角函数的有关公式化简后即可求模的最大值.
,然后直接运用求模公式求出模,运用三角函数的有关公式化简后即可求模的最大值.解答:解:(1)∵
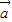 =(4cosα,sinα),
=(4cosα,sinα),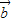 =(sinβ,4cosβ),由
=(sinβ,4cosβ),由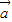 与
与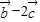 垂直,∴
垂直,∴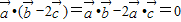 ,
,即4sin(α+β)-8cos(α+β)=0,∴tan(α+β)=2;
(2)∵
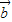 =(sinβ,4cosβ),
=(sinβ,4cosβ),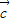 =(cosβ,4sinβ)
=(cosβ,4sinβ)则
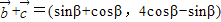 ,
,∴
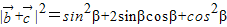 +16cos2β-32cosβsinβ+16sin2β
+16cos2β-32cosβsinβ+16sin2β=17-30sinβcosβ=17-15sin2β,最大值为32,所以
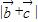 的最大值为4
的最大值为4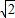 .
.点评:本题考查了运用数量积判断两个向量的垂直关系,考查了向量的模,考查了同角三角函数间的基本关系式,考查了学生的运算能力,此题是基础题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图,四边形ABCD中,E,F分别为AC、BD的中点,设向量
如图,四边形ABCD中,E,F分别为AC、BD的中点,设向量